题目内容
已知数列{an}满足an+1+an-1=2an(n∈N*,n≥2),且a3=7,a5+a7=26,{an}的前n项和为Sn.
(1)求an及Sn;
(2)令bn=
(n∈N*),数列{bn}的前n项和Tn,求证Tn<
.
(1)求an及Sn;
(2)令bn=
| 1 |
| an2-1 |
| 1 |
| 4 |
考点:数列递推式,数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)直接由数列递推式得到数列为等差数列,然后由已知列方程组求出首项和公差,代入等差数列的通项公式和前n项和公式得答案;
(2)把数列的通项公式代入bn=
,利用裂项相消法求和,再放缩得答案.
(2)把数列的通项公式代入bn=
| 1 |
| an2-1 |
解答:
(1)解:由数列{an}满足an+1+an-1=2an,可知数列{an}为等差数列,
设数列{an}的公差为d,
∵a3=7,a5+a7=26,
∴
,解得
.
∴an=3+2(n-1)=2n+1.
Sn=3n+
×2=n2+2n;
(2)证明:由(1)知an=2n+1.
∴bn=
=
=
•
=
(
-
).
∴Tn=
(1-
+
-
+…+
-
)=
(1-
).
当n→∞时,
→0.
故Tn<
.
设数列{an}的公差为d,
∵a3=7,a5+a7=26,
∴
|
|
∴an=3+2(n-1)=2n+1.
Sn=3n+
| n(n-1) |
| 2 |
(2)证明:由(1)知an=2n+1.
∴bn=
| 1 |
| an2-1 |
| 1 |
| (2n+1)2-1 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| n+1 |
当n→∞时,
| 1 |
| n+1 |
故Tn<
| 1 |
| 4 |
点评:本题考查了由等差中项的概念确定数列为等差数列,考查了等差数列的通项公式和前n项和公式,考查了裂项相消法求数列的和,训练了放缩法证明数列不等式,是中档题.

练习册系列答案
相关题目
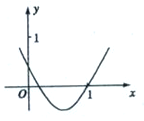 函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(2,3) |
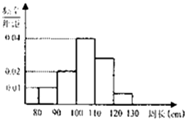 为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是
为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是