题目内容
观察下列各式71=7，72=49，73=343，74=2401，75=16807，…，则72014的末尾两位数是（ ）
| A、01 | B、43 | C、49 | D、07 |
考点：归纳推理
专题：规律型
分析：通过观察前几项，发现末两位数字分别为49、43、01、07、…，以4为周期出现重复，由此不难求出72014的末两位数字．
解答：
解：根据题意，得72=49，73=343，74=2401，75=16807，76=117649，77=823543，78=5764801，79=40353607…，
发现：74k-2的末两位数字是49，74k-1的末两位数字是43，74k的末两位数字是01，74k+1的末两位数字是49，（k=1、2、3、4、…）
∵2014=503×4…2，
∴72014的末两位数字为49，
故选：C．
发现：74k-2的末两位数字是49，74k-1的末两位数字是43，74k的末两位数字是01，74k+1的末两位数字是49，（k=1、2、3、4、…）
∵2014=503×4…2，
∴72014的末两位数字为49，
故选：C．
点评：本题以求7n（n≥2）的末两位数字的规律为载体，考查了数列的通项和归纳推理的一般方法的知识，属于基础题．
练习册系列答案
相关题目
已知α，β是两个不同的平面，?是一条直线，则下列命题中正确的是（ ）
| A、若α⊥β，??α，则?⊥β |
| B、若?∥α，α∥β，则?∥β |
| C、若?⊥α，?∥β，则α⊥β |
| D、若α⊥β，?⊥β，则?∥α |
已知a，b，c，d为偶数，且0＜a＜b＜c＜d，d-a=90，a，b，c成等差数列，b，c，d成等比数列，则a+b+c+d的值为（ ）
| A、384 | B、324 |
| C、284 | D、194 |
由若干个棱长为1的正方体搭成的几何体主视图和俯视图相同（如图所示），现给出如下四个图形，可能为侧视图的个数为（ ）
设函数f（x）=ex（sinx-cosx）（0≤x≤2014π），则函数f（x）的各极小值之和为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
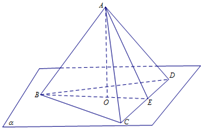如图，正三棱锥A-BCD放置在平面α上，AD=kCD，O是底面△BCD的中心，E是CD的中点，下列说法中，错误的是（ ）A、k＞
| ||||||||
B、当AD=CD=1时，将三棱锥绕直线AO旋转一周所形成的几何 体的体积是
| ||||||||
| C、动点P在截面ABE上运动，且到点B的距离与到点侧面ACD的距离相等，则点P在抛物线弧上 | ||||||||
D、当k=
|