题目内容
点P是△ABC所在平面外一点，O为点P在平面ABC内的射影，若PA=PB=PC，则点O是△ABC的 心．
考点：三角形五心
专题：空间位置关系与距离
分析：由点P在平面ABC上的投影为O，利用已知条件，结合勾股定理，证明出OA=OB=OC，进而根据三角形五心的定义，得到结论．
解答：
解：由点P作平面ABC的射影O，由题意：PA=PB=PC，
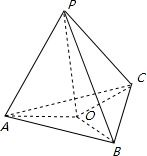
∵PO⊥底面ABC，
∴△PAO≌△POB≌△POC
即：OA=OB=OC
∴O为三角形的外心．
故答案为：外
∵PO⊥底面ABC，
∴△PAO≌△POB≌△POC
即：OA=OB=OC
∴O为三角形的外心．
故答案为：外
点评：本题考查棱锥的结构特征，三角形五心的定义，考查逻辑思维能力，是基础题．
练习册系列答案
相关题目
观察下列各式71=7，72=49，73=343，74=2401，75=16807，…，则72014的末尾两位数是（ ）
| A、01 | B、43 | C、49 | D、07 |
若α，β满足α-β=π，那么下列式子中正确的是（ ）
| A、sinα=sinβ |
| B、sinα=-sinβ |
| C、cosα=cosβ |
| D、cosα=sinβ |