题目内容
下列函数中，为奇函数的是（ ）
| A、y=x+1 |
| B、y=x2 |
| C、y=2x |
| D、y=x|x| |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：逐一判断各个选项中函数的奇偶性，可得结论．
解答：
解：由于y=x+1为非奇非偶函数，故排除A；
由于y=x2为偶函数，故排除B；
由于y=2x为非奇非偶函数，故排除C；
由于y=x|x|是奇函数，满足条件，
故选：D．
由于y=x2为偶函数，故排除B；
由于y=2x为非奇非偶函数，故排除C；
由于y=x|x|是奇函数，满足条件，
故选：D．
点评：本题主要考查函数的奇偶性的判断，属于基础题．
练习册系列答案
相关题目
已知点G是△ABC的外心，| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| A、一条线段 |
| B、一段圆弧 |
| C、椭圆的一部分 |
| D、抛物线的一部分 |
已知x，y满足
，且z=2x+y的最大值是最小值的4倍，则a的值是（ ）
|
| A、4 | ||
B、
| ||
C、
| ||
D、
|
函数y=sin（2x+
）图象的一条对称轴方程为（ ）
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
设i为虚数单位，复数
等于（ ）
| 2i |
| 1+i |
| A、-1+i | B、-1-i |
| C、1-i | D、1+i |
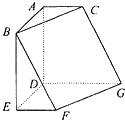如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，