题目内容
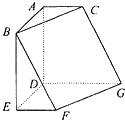如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，AB∥DE，EF∥DG，且AB=AD=DE=DG=2，AC=EF=1．
（1）求证：BF∥平面ACGD；
（2）求二面角D-CG-F的余弦值；
（3）求六面体ABCDEFG的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定,二面角的平面角及求法
专题：空间位置关系与距离,空间角
分析：几何法：
（1）取DG的中点M，连接AM、FM，由已知得四边形DEFM为平行四边形，从而得到四边形ABFM是平行四边形，由此能证明BF∥平面ACGD．
（2）由线面垂直DE⊥AD，又DE⊥DG，从而DE⊥平面ADGC，进而MF⊥平面ADGC．在平面ADGC中，过M作MN⊥GC，垂足为N，连接NF，则∠MNF是所求二面角的平面角，由此能求出二面角D-CG-F的余弦值．
（3）由题意六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，由此能求出六面体ABCDEFG的体积．
向量法：
（1）由AD，DE，DG两两垂直，以D为原点，建立空间直角坐标系，由向量量求出
=
，从而BF∥CG，由此能证明BF∥平面ACGD．
（2）求出平面BCGF的法向量和平面ACGD的法向量，由此利用向量法能注出二面角D-CG-F的余弦值．
（3）取DG的中点M，连接AM、FM，由题意可得六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，由此能求出六面体ABCDEFG的体积．
（1）取DG的中点M，连接AM、FM，由已知得四边形DEFM为平行四边形，从而得到四边形ABFM是平行四边形，由此能证明BF∥平面ACGD．
（2）由线面垂直DE⊥AD，又DE⊥DG，从而DE⊥平面ADGC，进而MF⊥平面ADGC．在平面ADGC中，过M作MN⊥GC，垂足为N，连接NF，则∠MNF是所求二面角的平面角，由此能求出二面角D-CG-F的余弦值．
（3）由题意六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，由此能求出六面体ABCDEFG的体积．
向量法：
（1）由AD，DE，DG两两垂直，以D为原点，建立空间直角坐标系，由向量量求出
| BF |
| CG |
（2）求出平面BCGF的法向量和平面ACGD的法向量，由此利用向量法能注出二面角D-CG-F的余弦值．
（3）取DG的中点M，连接AM、FM，由题意可得六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，由此能求出六面体ABCDEFG的体积．
解答：
（本小题满分14分）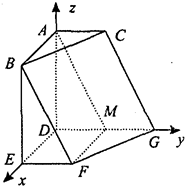
几何法：
（1）证明：如图，取DG的中点M，连接AM、FM．
因为DM=
DG=EF，且EF∥DM，
所以四边形DEFM为平行四边形．（1分）
所以MF∥DE，且MF=DE．（2分）
又AB∥DE，且AB=DE，所以MF∥AB，且MF=AB．（3分）
所以四边形ABFM是平行四边形，故BF∥AM．（4分）
又AM?平面ACGD，BF?平面ACGD，
所以BF∥平面ACGD．（5分）
（2）解：因为AD⊥平面DEFG，DE?平面DEFG，
所以DE⊥AD，又DE⊥DG，且AD∩DG=D，
所以DE⊥平面ADGC．
因为MF∥DE，所以MF⊥平面ADGC．（6分）
在平面ADGC中，过M作MN⊥GC，垂足为N，连接NF，
如图，则∠MNF是所求二面角的平面角．（7分）
因为在四边形ADGC中，
AD⊥AC，AD⊥DG，AC=DM=MG=1，
所以CD=CG=
，所以MN=
，（8分）
在Rt△MNF中，MF=2，MN=
，NF=
=
，（9分）
所以cos∠MNF=
=
，即二面角D-CG-F的余弦值为
．（10分）
（3）解：由题意及（1）与（2）可得：
六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，（12分）
所以V六面体ABCDEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG （13分）
=2×
×2×1+2×
×2×1=4．（14分）
向量法：
（1）证明：由已知可得AD，DE，DG两两垂直，
以D为原点，建立如图所示的空间直角坐标系，
则A（0，0，2），B（2，0，2），C（0，1，2），E（2，0，0），
F（2，1，0），G（0，2，0）．
=(0，1，-2)，
=（0，1，-2），
所以
=
，所以BF∥CG．（5分）
又CG?平面ACGD，BF?平面ACGD，所以BF∥平面ACGD． （6分）
（2）解：
=(0，2，0)，
设平面BCGF的法向量为
=（x，y，z），
则由
，得
，解得
，令z=1，得
=（1，2，1），（7分）
显然平面ACGD的法向量
=（1，0，0），（8分）
所以cos＜
，
＞=
=
，（9分）
故二面角D-CG-F的余弦值为
，（10分）
（3）解：取DG的中点M，连接AM、FM，
由题意可得六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，
所以V六面体ABCDEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG （13分）
=2×
×2×1+2×
×2×1=4．（14分）
几何法：
（1）证明：如图，取DG的中点M，连接AM、FM．
因为DM=
| 1 |
| 2 |
所以四边形DEFM为平行四边形．（1分）
所以MF∥DE，且MF=DE．（2分）
又AB∥DE，且AB=DE，所以MF∥AB，且MF=AB．（3分）
所以四边形ABFM是平行四边形，故BF∥AM．（4分）
又AM?平面ACGD，BF?平面ACGD，
所以BF∥平面ACGD．（5分）
（2）解：因为AD⊥平面DEFG，DE?平面DEFG，
所以DE⊥AD，又DE⊥DG，且AD∩DG=D，
所以DE⊥平面ADGC．
因为MF∥DE，所以MF⊥平面ADGC．（6分）
在平面ADGC中，过M作MN⊥GC，垂足为N，连接NF，
如图，则∠MNF是所求二面角的平面角．（7分）
因为在四边形ADGC中，
AD⊥AC，AD⊥DG，AC=DM=MG=1，
所以CD=CG=
| 5 |
2
| ||
| 5 |
在Rt△MNF中，MF=2，MN=
2
| ||
| 5 |
| M2F+M F |
2
| ||
| 5 |
所以cos∠MNF=
| MN |
| FN |
| ||
| 6 |
| ||
| 6 |
（3）解：由题意及（1）与（2）可得：
六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，（12分）
所以V六面体ABCDEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG （13分）
=2×
| 1 |
| 2 |
| 1 |
| 2 |
向量法：
（1）证明：由已知可得AD，DE，DG两两垂直，
以D为原点，建立如图所示的空间直角坐标系，
则A（0，0，2），B（2，0，2），C（0，1，2），E（2，0，0），
F（2，1，0），G（0，2，0）．
| BF |
| CG |
所以
| BF |
| CG |
又CG?平面ACGD，BF?平面ACGD，所以BF∥平面ACGD． （6分）
（2）解：
| FG |
设平面BCGF的法向量为
| n1 |
则由
|
|
|
| n1 |
显然平面ACGD的法向量
| n2 |
所以cos＜
| n1 |
| n2 |
| ||||
|
|
| ||
| 6 |
故二面角D-CG-F的余弦值为
| ||
| 6 |
（3）解：取DG的中点M，连接AM、FM，
由题意可得六面体ABCDEFG可分割成直三棱柱ADM-BEF和斜三棱柱ABC-MFG，
所以V六面体ABCDEFG=V三棱柱ADM-BEF+V三棱柱ABC-MFG （13分）
=2×
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题考查线面垂直的证明，考查二面角的余弦值的求法，考查六面体的体积的求法，是中档题，解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用．
练习册系列答案
相关题目
下列函数中，为奇函数的是（ ）
| A、y=x+1 |
| B、y=x2 |
| C、y=2x |
| D、y=x|x| |
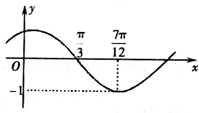函数f（x）=Asin（ωx+φ）（其中A＞0，ω，0，|φ|＜| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
某几何体的三视图如图所示，则该几何体的体积是（ ）
| A、2 | B、≥ | C、∞ | D、3 |
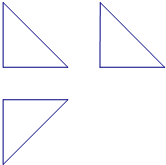如图，某三棱锥的三视图都是直角边为| 2 |
A、
| ||
| B、6π | ||
C、2
| ||
| D、8π |
四边形ABCD是单位圆O的内接正方形，它可以绕原点O转动，已知点P的坐标是（3，4），M、N分别是边AB、BC的中点，则