题目内容
已知点G是△ABC的外心，| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| A、一条线段 |
| B、一段圆弧 |
| C、椭圆的一部分 |
| D、抛物线的一部分 |
考点：轨迹方程
专题：计算题,直线与圆
分析：确定点G是BC的中点，△ABC是直角三角形，∠A是直角，BC=2，根据△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动，即可得出结论．
解答：
解：∵点G是△ABC的外心，且2
+
+
=
，|
∴点G是BC的中点，△ABC是直角三角形，∠A是直角
∵
，
，
是三个单位向量，
∴BC=2
∵△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动
∴G的轨迹是以原点为圆心1为半径的圆弧，
故选：B．
| GA |
| AB |
| AC |
| 0 |
∴点G是BC的中点，△ABC是直角三角形，∠A是直角
∵
| GA |
| GB |
| GC |
∴BC=2
∵△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动
∴G的轨迹是以原点为圆心1为半径的圆弧，
故选：B．
点评：本题考查向量在几何中的应用，解题的关键是判断三角形的形状，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若函数f（x）=
x3-
x2+
x+1在x=1处的切线的倾斜角为α，则
的值是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| cos2α |
| sin2α-cos2α |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设|
|=1，|
|=2，且
，
夹角为
，则|2
+
|=（ ）
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| A、2 | ||
| B、4 | ||
| C、12 | ||
D、2
|
下列说法中正确的是（ ）
①若一个平面内的任何直线都与另一个平面无公共点，则这两个平面平行；
②过平面外一点有且仅有一个平面和已知平面平行；
③过平面外两点不能作平面与已知平面平行；
④若一条直线和一个平面平行，经过这条直线的任何平面都与已知平面平行．
①若一个平面内的任何直线都与另一个平面无公共点，则这两个平面平行；
②过平面外一点有且仅有一个平面和已知平面平行；
③过平面外两点不能作平面与已知平面平行；
④若一条直线和一个平面平行，经过这条直线的任何平面都与已知平面平行．
| A、①③ | B、②④ | C、①② | D、③④ |
已知不等式组
所表示的平面区域为D，若直线y=kx-3与平面区域D有公共点，则k的取值范围是（ ）
|
| A、[-3，3] | ||||
B、（-∞，
| ||||
| C、（-∞，-3]∪[3，+∞） | ||||
D、[-
|
下列函数中，为奇函数的是（ ）
| A、y=x+1 |
| B、y=x2 |
| C、y=2x |
| D、y=x|x| |
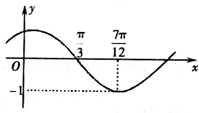函数f（x）=Asin（ωx+φ）（其中A＞0，ω，0，|φ|＜| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|