题目内容
计算:sin72°cos27°-sin18°cos63°= .
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:根据两角和差的正弦公式以及三角函数的诱导公式进行化简即可.
解答:
解:sin72°cos27°-sin18°cos63°=sin72°cos27°-cos72°sin27°=sin(72°-27°)
=sin45°=
,
故答案为:
=sin45°=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查三角函数的求值,利用两角和差的正弦公式以及三角函数的诱导公式是解决本题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
①若一个平面内的任何直线都与另一个平面无公共点,则这两个平面平行;
②过平面外一点有且仅有一个平面和已知平面平行;
③过平面外两点不能作平面与已知平面平行;
④若一条直线和一个平面平行,经过这条直线的任何平面都与已知平面平行.
①若一个平面内的任何直线都与另一个平面无公共点,则这两个平面平行;
②过平面外一点有且仅有一个平面和已知平面平行;
③过平面外两点不能作平面与已知平面平行;
④若一条直线和一个平面平行,经过这条直线的任何平面都与已知平面平行.
| A、①③ | B、②④ | C、①② | D、③④ |
下列函数中,为奇函数的是( )
| A、y=x+1 |
| B、y=x2 |
| C、y=2x |
| D、y=x|x| |
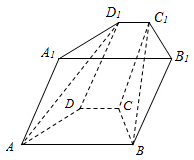 如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.
如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.