题目内容
已知
=(2cosx+2
sinx,1),
=(cosx,-y),且
⊥
.
(1)将y表示为x的函数f(x),并求f(x)的对称轴的方程;
(2)若函数y=f(x)的图象在y轴右侧的最高点的横坐标组成一个数列{an},求a1+a2+…+a2015的值.
| m |
| 3 |
| n |
| m |
| n |
(1)将y表示为x的函数f(x),并求f(x)的对称轴的方程;
(2)若函数y=f(x)的图象在y轴右侧的最高点的横坐标组成一个数列{an},求a1+a2+…+a2015的值.
考点:数列的求和,数量积判断两个平面向量的垂直关系
专题:等差数列与等比数列
分析:(1)由已知利用向量垂直的性质和三角函数知识,得y=2cos2x+2
sinxcosx=2sin(2x+
)+1,由此能求出f(x)的对称轴的方程.
(2)由三角函数的性质得an=
+2(n-1)π,n∈N*,由此能求出a1+a2+…+a2015的值.
| 3 |
| π |
| 6 |
(2)由三角函数的性质得an=
| π |
| 2 |
解答:
解:(1)∵
=(2cosx+2
sinx,1),
=(cosx,-y),且
⊥
,
∴
•
=2cos2x+2
sinxcosx-y=0,
∴y=2cos2x+2
sinxcosx
=
sin2x+cos2x+1
=2sin(2x+
)+1,
f(x)的对称轴的方程为:2x+
=kπ+
,k∈Z,
整理,得x=
+
,k∈Z.
(2)∵y=2sin(2x+
)+1,∴当2x+
=
+2kπ,k∈Z时,y取最大值3,
∵函数y=f(x)的图象在y轴右侧的最高点的横坐标组成一个数列{an},
∴an=
+2(n-1)π,n∈N*,
∴a1+a2+…+a2015=
×2015+2(1+2+3+…+2014)π
=
+2014×2015π
=4059217.5π.
| m |
| 3 |
| n |
| m |
| n |
∴
| m |
| n |
| 3 |
∴y=2cos2x+2
| 3 |
=
| 3 |
=2sin(2x+
| π |
| 6 |
f(x)的对称轴的方程为:2x+
| π |
| 6 |
| π |
| 2 |
整理,得x=
| kπ |
| 2 |
| π |
| 6 |
(2)∵y=2sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∵函数y=f(x)的图象在y轴右侧的最高点的横坐标组成一个数列{an},
∴an=
| π |
| 2 |
∴a1+a2+…+a2015=
| π |
| 2 |
=
| 2015π |
| 2 |
=4059217.5π.
点评:本题考查函数解析式的求法,考查数列的前2015项和的求法,是中档题,解题时要认真审题,注意三角函数性质的合理运用.

练习册系列答案
相关题目
若函数f(x)=
x3-
x2+
x+1在x=1处的切线的倾斜角为α,则
的值是( )
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| cos2α |
| sin2α-cos2α |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设|
|=1,|
|=2,且
,
夹角为
,则|2
+
|=( )
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| A、2 | ||
| B、4 | ||
| C、12 | ||
D、2
|
下列函数中,为奇函数的是( )
| A、y=x+1 |
| B、y=x2 |
| C、y=2x |
| D、y=x|x| |
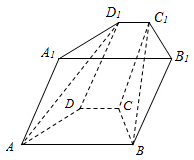 如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.
如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.