题目内容
已知x,y满足
,且z=2x+y的最大值是最小值的4倍,则a的值是( )
|
| A、4 | ||
B、
| ||
C、
| ||
D、
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组
对应的平面区域,利用z的几何意义,结合目标函数z=2x+y的最大值是最小值的4倍,建立方程关系,即可得到结论.
|
解答:
解:作出不等式组
对应的平面区域如图: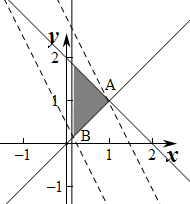
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线的截距最大,
此时z最大,
由
,解得
即A(1,1),此时z=2×1+1=3,
当直线y=-2x+z经过点B时,直线的截距最小,
此时z最小,
由
,解得
,
即B(a,a),此时z=2×a+a=3a,
∵目标函数z=2x+y的最大值是最小值的4倍,
∴3=4×3a,
即a=
.
故选:D.
|

由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线的截距最大,
此时z最大,
由
|
|
当直线y=-2x+z经过点B时,直线的截距最小,
此时z最小,
由
|
|
即B(a,a),此时z=2×a+a=3a,
∵目标函数z=2x+y的最大值是最小值的4倍,
∴3=4×3a,
即a=
| 1 |
| 4 |
故选:D.
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
设|
|=1,|
|=2,且
,
夹角为
,则|2
+
|=( )
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| A、2 | ||
| B、4 | ||
| C、12 | ||
D、2
|
已知不等式组
所表示的平面区域为D,若直线y=kx-3与平面区域D有公共点,则k的取值范围是( )
|
| A、[-3,3] | ||||
B、(-∞,
| ||||
| C、(-∞,-3]∪[3,+∞) | ||||
D、[-
|
下列函数中,为奇函数的是( )
| A、y=x+1 |
| B、y=x2 |
| C、y=2x |
| D、y=x|x| |
已知i为虚数单位,则复数z=(-1-2i)i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |