题目内容
函数f(x)=logax+x-2有两个零点x1,x2,其中x1∈(0,1),x2∈(2,3),则实数a的取值范围是( )
A、(0,
| ||
B、(
| ||
| C、(1,3) | ||
| D、(3,+∞) |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据函数的额零点就是方程的解也是两个函数的图象的交点的横坐标,再根据对数函数的性质,得到不等式组,解得即可.
解答:
解:∵函数f(x)=logax+x-2有两个零点x1,x2,
∴f(x)=logax+x-2=0的两个根是x1,x2,
即y=logax与y=-x+2的图象的两个交点的横坐标为x1,x2,满足x1∈(0,1),x2∈(2,3),
∴
,
解得0<a<
,
故实数a的取值范围是(0,
),
故选:A
∴f(x)=logax+x-2=0的两个根是x1,x2,
即y=logax与y=-x+2的图象的两个交点的横坐标为x1,x2,满足x1∈(0,1),x2∈(2,3),
∴
|
解得0<a<
| 1 |
| 3 |
故实数a的取值范围是(0,
| 1 |
| 3 |
故选:A
点评:本题主要考查了函数的零点和图象的交点的关系,以及对数函数的性质,属于基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,如果输出的p是720,那么输入的整数N是( )


| A、5 | B、6 | C、7 | D、8 |
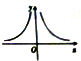 已知幂函数f(x)=xn-2(n∈N)的图象如图所示,则y=f(x)在x=1处的切线与两坐标轴围成的面积为( )
已知幂函数f(x)=xn-2(n∈N)的图象如图所示,则y=f(x)在x=1处的切线与两坐标轴围成的面积为( )A、
| ||
B、
| ||
C、
| ||
| D、4 |
已知集合A={x|y=-
},B={(x,y)|y=2x,x>0},R是实数集,(∁RB)∩A=( )
| 2x-x2 |
| A、Φ | B、R |
| C、(1,2] | D、[0,1] |