题目内容
3.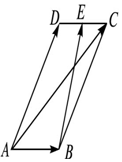 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
分析 由条件并结合图形可得到$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,$\overrightarrow{BE}=-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$,这样代入$\overrightarrow{AC}•\overrightarrow{BE}$进行数量积的运算即可得出$-\frac{1}{2}|\overrightarrow{AB}{|}^{2}+\frac{1}{4}|\overrightarrow{AB}|+1=\frac{33}{32}$,解该方程即可求出AB的长.
解答 解:根据条件:
$\overrightarrow{AC}•\overrightarrow{BE}=(\overrightarrow{AB}+\overrightarrow{AD})•(\overrightarrow{BC}+\overrightarrow{CE})$
=$(\overrightarrow{AB}+\overrightarrow{AD})•(-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD})$
=$-\frac{1}{2}{\overrightarrow{AB}}^{2}+\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AD}+{\overrightarrow{AD}}^{2}$
=$-\frac{1}{2}|\overrightarrow{AB}{|}^{2}+\frac{1}{4}|\overrightarrow{AB}|+1$
=$\frac{33}{32}$;
∴$16|\overrightarrow{AB}{|}^{2}-8|\overrightarrow{AB}|+1=0$;
解得$|\overrightarrow{AB}|=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 考查向量加法的平行四边形法则,向量加法、数乘的几何意义,相等向量和相反向量的概念,向量数量积的运算.

| A. | $\frac{1}{7}$ | B. | ±$\frac{1}{7}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | ±$\frac{\sqrt{2}}{10}$ |
| A. | 4个 | B. | 6个 | C. | 7个 | D. | 8个 |
| A. | x=-8y2 | B. | y=-8x2 | C. | x=-16y2 | D. | y=-16x2 |
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 奇偶性与k的值有关 |
 某工艺品厂要设计一个如图Ⅰ所示的工艺品,现有某种型号的长方形材料如图Ⅱ所示,其周长为4m,这种材料沿其对角线折叠后就出现图Ⅰ的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为
某工艺品厂要设计一个如图Ⅰ所示的工艺品,现有某种型号的长方形材料如图Ⅱ所示,其周长为4m,这种材料沿其对角线折叠后就出现图Ⅰ的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为