题目内容
12.已知f(x)在R上是增函数,且f(2)=0,则使f(x-2)>0成立的x的取值范围是(4,+∞).分析 由条件利用函数的单调性的性质可得x-2>2,由此求得x的取值范围.
解答 解:∵f(x)在R上是增函数,且f(2)=0,要使f(x-2)>0,
则有x-2>2,即 x>4,成立的x的取值范围是(4,+∞),
故答案为:(4,+∞).
点评 本题主要考查函数的单调性的性质,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A,B两点,直线AF2与椭圆的另一个交点为C,若$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}C}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{3}}{10}$ |
7.下面四组函数中,f(x)与g(x)表示同一个函数的是( )
| A. | f(x)=|x|,$g(x)={({\sqrt{x}})^2}$ | B. | f(x)=2x,$g(x)=\frac{{2{x^2}}}{x}$ | C. | f(x)=x,$g(x)=\root{3}{x^3}$ | D. | f(x)=x,$g(x)=\frac{1}{{\sqrt{x^2}}}$ |
2.已知lg5=m,lg7=n,则log27=( )
| A. | $\frac{m}{n}$ | B. | $\frac{n}{1-m}$ | C. | $\frac{1-n}{m}$ | D. | $\frac{1+n}{1+m}$ |
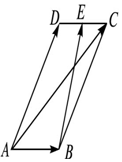 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.