题目内容
8.已知三个不等式:①ab<0;②$-\frac{c}{a}<-\frac{d}{b}$;③bc<ad,以其中两个为条件,余下的一个作为结论,则可以组成3个正确的命题.分析 结合不等式的基本性质,逐一分析以其中两个为条件,余下的一个作为结论,构造的命题的真假,可得答案.
解答 解:当①ab<0;②$-\frac{c}{a}<-\frac{d}{b}$时,
②两边同乘-ab得:bc<ad,
即①②⇒③正确;
当①ab<0;③bc<ad,时,
③两边同除以-ab得:$-\frac{c}{a}<-\frac{d}{b}$,
即①③⇒②正确;
当②$-\frac{c}{a}<-\frac{d}{b}$;③bc<ad时,ab<0,
即②③⇒①正确;
故正确的命题有3个,
故答案为:3.
点评 本题以命题的真假判断与应用为载体,考查了不等式的基本性质,难度中档.

练习册系列答案
相关题目
16.已知椭圆$\frac{x^2}{4}+\frac{y^2}{20}$=1的焦点坐标为 ( )
| A. | (±4,0) | B. | (±2,0) | C. | (0,±4) | D. | (0,±2) |
13.已知tanα>0,则点P(sinα,cosα)位于( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
20.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A,B两点,直线AF2与椭圆的另一个交点为C,若$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}C}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{3}}{10}$ |
18.已知等差数列{an},Sn为其前n项和,若a1=9,a3+a5=0,则S6的值为( )
| A. | 6 | B. | 9 | C. | 15 | D. | 0 |
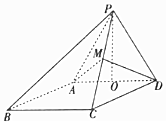 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.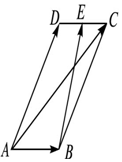 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.