��Ŀ����
13�� ij����Ʒ��Ҫ���һ����ͼ����ʾ�Ĺ���Ʒ������ij���ͺŵij����β�����ͼ����ʾ�����ܳ�Ϊ4m�����ֲ�������Խ����۵���ͳ���ͼ����������ͼ��ABCD��AB��AD��Ϊ�����εIJ��ϣ���AC�۵���AB'��DC�ڵ�P�����ADP�����Ϊ
ij����Ʒ��Ҫ���һ����ͼ����ʾ�Ĺ���Ʒ������ij���ͺŵij����β�����ͼ����ʾ�����ܳ�Ϊ4m�����ֲ�������Խ����۵���ͳ���ͼ����������ͼ��ABCD��AB��AD��Ϊ�����εIJ��ϣ���AC�۵���AB'��DC�ڵ�P�����ADP�����ΪS2���۵����غϲ��֡�ACP�����ΪS1��
������AB=xm����x��ʾͼ��DP�ij��ȣ���д��x��ȡֵ��Χ��
���������S2���ʱ��Ӧ������Ʋ��ϵij��Ϳ���
�����������S1+2S2�����ʱ��Ӧ������Ʋ��ϵij��Ϳ���
���� ������AB=xm�����á�ADP�ա�CB'P����PA=PC=x-y�����PA2=AD2+DP2��������x��ʾͼ��DP�ij��ȣ���д��x��ȡֵ��Χ��
�������û�������ʽ�����S2���ʱ����Ʋ��ϵij��Ϳ���
�����������S1+2S2�������õ���ȷ�������ĵ����ԣ����ɵó����ʱ����Ʋ��ϵij��Ϳ���
��� �⣺���������⣬AB=x��BC=2-x��
��Ϊx��2-x����1��x��2������2�֣�
��DP=y����PC=x-y��
��Ϊ��ADP�ա�CB'P����PA=PC=x-y��
��PA2=AD2+DP2���ã�x-y��2=��2-x��2+y2��$y=2��{1-\frac{1}{x}}����1��x��2$������4�֣�
���ǡ�ADP�����ΪS2����${S_2}=��{1-\frac{1}{x}}����{2-x}��$����5�֣�
=$3-��{x+\frac{2}{x}}����3-2\sqrt{2}$��
���ҽ���$x=\sqrt{2}�ʣ�{1��2}��$ʱ��S2ȡ�����ֵ������7�֣�
�ʵ����ϳ�Ϊ$\sqrt{2}m$����Ϊ$��{2-\sqrt{2}}��m$ʱ��S2�����8�֣�
����${S_1}+2{S_2}=\frac{1}{2}x��{2-x}��+��{1-\frac{1}{x}}����{2-x}��=3-\frac{1}{2}��{{x^2}+\frac{4}{x}}��$��1��x��2��
����$��{{S_1}+2{S_2}}��'=-\frac{1}{2}��{2x-\frac{4}{x^2}}��=\frac{{-{x^3}+2}}{x^2}=0$����$x=\root{3}{2}$������11�֣�
����x�ĺ�����S1+2S2����$��{1��\root{3}{2}}��$�ϵ�������$��{\root{3}{2}��2}��$�ϵݼ���
���Ե�$x=\root{3}{2}$ʱ��S1+2S2ȡ�����ֵ������12�֣�
�ʵ����ϳ�Ϊ$\root{3}{2}$m����Ϊ$��{2-\root{3}{2}}��$mʱ��S1+2S2�����13�֣�
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬�����������ʽ������֪ʶ�����ã�ȷ�������ı���ʽ�ǹؼ���

| A�� | 16 | B�� | 8 | C�� | 4 | D�� | 1 |
| A�� | 6 | B�� | 9 | C�� | 15 | D�� | 0 |
| A�� | $\frac{m}{n}$ | B�� | $\frac{n}{1-m}$ | C�� | $\frac{1-n}{m}$ | D�� | $\frac{1+n}{1+m}$ |
| A�� |  | B�� | 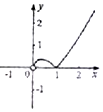 | C�� |  | D�� |  |
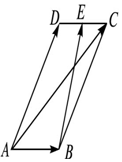 ��ƽ���ı���ABCD�У�AD=1����BAD=60�㣬EΪCD���е㣮��$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$����AB�ij�Ϊ$\frac{1}{4}$��
��ƽ���ı���ABCD�У�AD=1����BAD=60�㣬EΪCD���е㣮��$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$����AB�ij�Ϊ$\frac{1}{4}$��