题目内容
11.满足{-1,0,1}?M⊆{-1,0,1,2,3,4}的集合M的个数是( )| A. | 4个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 由{-1,0,1}?M⊆{-1,0,1,2,3,4},知集合M中必有元素-1,0,1,并且还有元素2,3,4中的1个或2个或3个,由此能求出满足条件的集合M的个数.
解答 解:∵{-1,0,1}?M⊆{-1,0,1,2,3,4},
∴M={-1,0,1,2}或M={-1,0,1,3}或M={-1,0,1,4}或M={-1,0,1,2,3}或M={-1,0,1,2,4}或M={-1,0,1,3,4}或M={-1,0,1,2,3,4},
故有7个,
故选C.
点评 本题考查集合的包含关系的判断及其应用,解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知椭圆$\frac{x^2}{4}+\frac{y^2}{20}$=1的焦点坐标为 ( )
| A. | (±4,0) | B. | (±2,0) | C. | (0,±4) | D. | (0,±2) |
20.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A,B两点,直线AF2与椭圆的另一个交点为C,若$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}C}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{3}}{10}$ |
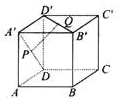 如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.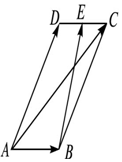 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.