题目内容
14.函数f(x)=$\left\{\begin{array}{l}{{x^2}-2x,x≥-1}\\{x+4,x<-1}\end{array}}$,若函数g(x)=f(x)-a有三个零点,则a的取值范围为(-1,3).分析 函数g(x)=f(x)-a有三个零点,可知函数y=f(x)与y=a有三个交点,作出分段函数的图象,数形结合得答案.
解答 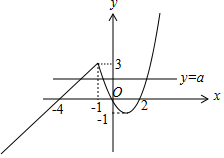 解:作出函数f(x)=$\left\{\begin{array}{l}{{x^2}-2x,x≥-1}\\{x+4,x<-1}\end{array}}$的图象如图,
解:作出函数f(x)=$\left\{\begin{array}{l}{{x^2}-2x,x≥-1}\\{x+4,x<-1}\end{array}}$的图象如图,
函数y=x+4 在 x∈(-∞,-1)上单调增,其值域为(-∞,3];
函数y=x2-2x(x≥-1)在[-1,1]上是递减,在[1,+∞)递增,
其值域为[-1,3],
∴要使函数g(x)=f(x)-a有三个零点,由图可知a的取值范围为(-1,3).
故答案为:(-1,3).
点评 本题考查了分段函数的零点问题,转化为函数交点问题是常见方法,属于中档题.

练习册系列答案
相关题目
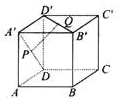 如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.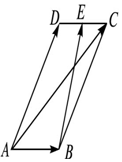 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.