题目内容
13.若tanα=$\frac{1}{3}$,tan(α+β)=$\frac{1}{2}$,则sinβ=( )| A. | $\frac{1}{7}$ | B. | ±$\frac{1}{7}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | ±$\frac{\sqrt{2}}{10}$ |
分析 由两角和与差的正切函数求得tanβ的值,然后结合同角三角函数关系来求sinβ的值.
解答 解:∵tanα=$\frac{1}{3}$,tan(α+β)=$\frac{1}{2}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=$\frac{\frac{1}{3}+tanβ}{1-\frac{1}{3}tanβ}$=$\frac{1}{2}$,
则tanβ=$\frac{2}{5}$,
∴$\frac{sinβ}{cosβ}$=$\frac{2}{5}$,①
又sin2β+cos2β=1,②,
联立①②得到:sinβ=±$\frac{\sqrt{2}}{10}$.
故选:D.
点评 此题考查了两角和与差的正切函数公式,以及同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
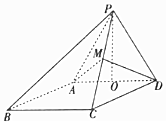 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.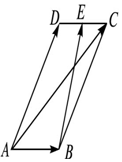 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.