题目内容
18.已知抛物线的焦点坐标为(-$\frac{1}{32}$,0),则抛物线的标准方程为( )| A. | x=-8y2 | B. | y=-8x2 | C. | x=-16y2 | D. | y=-16x2 |
分析 利用抛物线的焦点坐标,求解抛物线方程即可.
解答 解:抛物线的焦点坐标为(-$\frac{1}{32}$,0),
则抛物线的标准方程为:x=-8y2.
故选:A.
点评 本题考查抛物线方程的求法,考查计算能力.

练习册系列答案
相关题目
10.已知函数$f(x)=\frac{1}{{1+{x^2}}}$,则$f(2016)+f(2015)+…+f(2)+f(\frac{1}{2})+…+f(\frac{1}{2015})$$+f(\frac{1}{2016})$的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
7.下面四组函数中,f(x)与g(x)表示同一个函数的是( )
| A. | f(x)=|x|,$g(x)={({\sqrt{x}})^2}$ | B. | f(x)=2x,$g(x)=\frac{{2{x^2}}}{x}$ | C. | f(x)=x,$g(x)=\root{3}{x^3}$ | D. | f(x)=x,$g(x)=\frac{1}{{\sqrt{x^2}}}$ |
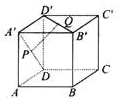 如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.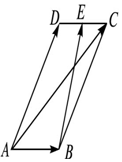 在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.
在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,则AB的长为$\frac{1}{4}$.