题目内容
已知函数f(x)=2+log2x,x∈[1,8],求函数y=[f(x)]2+f(x2)的最大值及此时x的值.
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:由x2∈[1,8],可推出log2x的范围,化简函数y,运用配方即可得到最值.
解答:
解:∵x∈[1,8],且x2∈[1,8],
∴x∈[1,2
],
∴0≤t=log2x≤
,
又∵[f(x)]2+f(x2)=(2+log2x)2+2+2log2x
=(2+t)2+2+2t=t2+6t+6=(t+3)2-3,
则当t=
,即x=2
,y取最大值,且为
.
∴x∈[1,2
| 2 |
∴0≤t=log2x≤
| 3 |
| 2 |
又∵[f(x)]2+f(x2)=(2+log2x)2+2+2log2x
=(2+t)2+2+2t=t2+6t+6=(t+3)2-3,
则当t=
| 3 |
| 2 |
| 2 |
| 69 |
| 4 |
点评:本题实质考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
相关题目
已知m>0,n>0,且2m+3n=5,则
+
的最小值是( )
| 2 |
| m |
| 3 |
| n |
| A、25 | ||
B、
| ||
| C、4 | ||
| D、5 |
如图程序框图中,若输出S=
+
,则p的值为( )
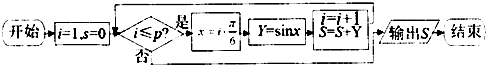
| 3 |
| 2 |
| 3 |
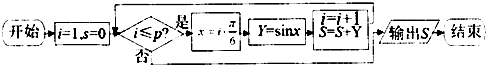
| A、3 | B、4 | C、5 | D、6 |
下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
| A、y=x3 |
| B、y=|x|+1 |
| C、y=-x2+1 |
| D、y=2x+1 |