题目内容
设f(x)=x2+px+q,集合A={x|x=f(x)},B={x|f[f(x)]=x},
(1)求证:A⊆B;
(2)若集合A={-1,3},求集合B.
(1)求证:A⊆B;
(2)若集合A={-1,3},求集合B.
考点:集合的包含关系判断及应用
专题:集合
分析:(1)若x∈A,则x=f(x)成立,则f[f(x)]=f(x)=x必成立,进而根据集合包含关系的定义,得到结论;
(2)由A={x|f(x)=x}={x|x2+px+q=x}={x|x2+(p-1)x+q=0}={-1,3},结合方程根与系数关系可求p,q,进而可求,f(x),然后代入B={x|f[f(x)]=x}整理可求
(2)由A={x|f(x)=x}={x|x2+px+q=x}={x|x2+(p-1)x+q=0}={-1,3},结合方程根与系数关系可求p,q,进而可求,f(x),然后代入B={x|f[f(x)]=x}整理可求
解答:
证明:(1)若x∈A,
则x=f(x)成立,
则f[f(x)]=f(x)=x必成立,
即x∈B,
故A⊆B;
(2)∵A={x|f(x)=x}={x|x2+px+q=x}={x|x2+(p-1)x+q=0}={-1,3}
∴-1,3是方程x2+(p-1)x+q=0的根
∴
,即p=-1,q=-3,f(x)=x2-x-3
∴B={x|f[f(x)]=x}={x|f(x2-x-3)=x}={x|(x2-x-3)2-(x2-x-3)-3=x}
化简可得,(x2-x-3)2-x2=0
∴(x2-3)(x2-2x-3)=0
∴x=
或x=-
或x=3或x=-1
∴B={
,-
,-1,3}
则x=f(x)成立,
则f[f(x)]=f(x)=x必成立,
即x∈B,
故A⊆B;
(2)∵A={x|f(x)=x}={x|x2+px+q=x}={x|x2+(p-1)x+q=0}={-1,3}
∴-1,3是方程x2+(p-1)x+q=0的根
∴
|
∴B={x|f[f(x)]=x}={x|f(x2-x-3)=x}={x|(x2-x-3)2-(x2-x-3)-3=x}
化简可得,(x2-x-3)2-x2=0
∴(x2-3)(x2-2x-3)=0
∴x=
| 3 |
| 3 |
∴B={
| 3 |
| 3 |
点评:本题主要考查了二次函数与二次方程之间关系的相互转化,方程的根与系数关系的应用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
等差数列{an}满足an∈N*,且前10项和S10=280,则a9最大值是( )
| A、28 | B、49 | C、50 | D、52 |
一个扇形的弧长与面积都是5,则这个扇形圆心角的弧度数为( )
| A、2rad | ||
B、
| ||
| C、1rad | ||
D、
|
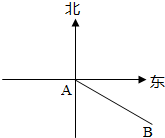 已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.
已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.