��Ŀ����
������R�ϵĺ���f��x������ͼ�����������ϵģ�������ڷ��㳣���ˣ��ˡ�R����ʹ�ö������x��R������f��x+�ˣ�=��f��x�������f��x��Ϊ����������������Ϊ������ϵ����������������ȷ���� ��д��������ȷ����ı�ţ���
�ٺ���f��x��=x�DZ����������ұ���ϵ����=1��
�ں���f��x��=e-x�DZ����������ұ���ϵ���ˡʣ�0��1����
��������f��x���ǿɵ��������������䵼����f�䣨x��Ҳ�DZ���������
��������f��x���DZ���ϵ����=-1�ı�����������f��x��Ҳ�����ں�����
��������f��x��=cos2��x���أ�0���DZ������������=
��k��N*����
�ٺ���f��x��=x�DZ����������ұ���ϵ����=1��
�ں���f��x��=e-x�DZ����������ұ���ϵ���ˡʣ�0��1����
��������f��x���ǿɵ��������������䵼����f�䣨x��Ҳ�DZ���������
��������f��x���DZ���ϵ����=-1�ı�����������f��x��Ҳ�����ں�����
��������f��x��=cos2��x���أ�0���DZ������������=
| k�� |
| 2 |
���㣺����������Ӧ��,������������
ר�⣺�¶���,���������ʼ�Ӧ��
�������ٸ��ݱ��������Ķ��壬�����жϣ�
���ɱ��������Ķ��壬���ָ��������ֵ�����жϣ�
���ɱ��������Ķ��壬�����������жϣ�
�����ñ��������Ķ��壬�����ν�x����x+1������������ڣ����жϣ�
�����ñ��������Ķ��壬Ȼ��ֱ���x=0����x=
��������Ǻ͵����ҹ�ʽ����������أ��Ӷ��жϣ�
���ɱ��������Ķ��壬���ָ��������ֵ�����жϣ�
���ɱ��������Ķ��壬�����������жϣ�
�����ñ��������Ķ��壬�����ν�x����x+1������������ڣ����жϣ�
�����ñ��������Ķ��壬Ȼ��ֱ���x=0����x=
| �� |
| 2 |
���
�⣺�١�f��x��=x��f��x+�ˣ�=x+�ˣ���f��x��=��x������ڦˡ�0��?x��R����f��x+�ˣ�=��f��x�����ʢٴ���
�ڡߺ���f��x��=e-x�DZ�����������e-��x+�ˣ�=��e-x����e-��=�ˣ�0�����=
�ʣ�0��1�����ʢ���ȷ��
�ۡ�f��x������?�ˡ�0��?x��R��f��x+�ˣ�=��f��x������f�䣨x+�ˣ�=��f�䣨x����������ʢ���ȷ��
��������f��x���DZ���ϵ����=-1�ı�����������f��x-1��=-f��x������f��x��=-f��x+1����
��f��x+2��=-f��x+1��=f��x����������f��x��Ϊ����Ϊ2�ĺ������ʢ���ȷ��
�ݡ�f��x��=cos��2��x�����أ�0���DZ���������
��cos[2�أ�x+�ˣ�]=��cos��2��x������x=0��cos��2�ئˣ�=�ˣ�
��x=
����cos[2�أ�
+�ˣ�]=��cos��2��•
���������sin�ئ�sin2�ئ�=0��
����=k��
��k��N*����ʢݲ���ȷ��
�ʴ�Ϊ���ڢۢܣ�
�ڡߺ���f��x��=e-x�DZ�����������e-��x+�ˣ�=��e-x����e-��=�ˣ�0�����=
| 1 |
| e�� |
�ۡ�f��x������?�ˡ�0��?x��R��f��x+�ˣ�=��f��x������f�䣨x+�ˣ�=��f�䣨x����������ʢ���ȷ��
��������f��x���DZ���ϵ����=-1�ı�����������f��x-1��=-f��x������f��x��=-f��x+1����
��f��x+2��=-f��x+1��=f��x����������f��x��Ϊ����Ϊ2�ĺ������ʢ���ȷ��
�ݡ�f��x��=cos��2��x�����أ�0���DZ���������
��cos[2�أ�x+�ˣ�]=��cos��2��x������x=0��cos��2�ئˣ�=�ˣ�
��x=
| �� |
| 2 |
| �� |
| 2 |
| �� |
| 2 |
����=k��
| k�� |
| 2 |
�ʴ�Ϊ���ڢۢܣ�
���������⿼���¶��壺�������������ʣ����麯���������ԡ�ֵ����ʱҪ�������⣬��ϸ���ע������ؽ��еȼ�ת����

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��A��
��ͼ��A��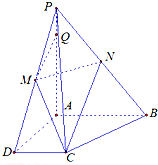 ��֪����P-ABCD�У�PA��ƽ��ABCD����PA=4������Ϊֱ�����Σ���CDA=��BAD=90�㣬AB=2��CD=1��AD=
��֪����P-ABCD�У�PA��ƽ��ABCD����PA=4������Ϊֱ�����Σ���CDA=��BAD=90�㣬AB=2��CD=1��AD=