题目内容
(本小题满分14分)已知函数 =
=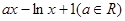 ,
,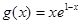 .
.
(1)求函数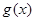 在区间
在区间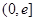 上的值域;
上的值域;
(2)是否存在实数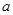 ,对任意给定的
,对任意给定的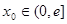 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的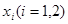 ,使得
,使得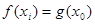 成立.若存在,求出
成立.若存在,求出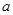 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(3)给出如下定义:对于函数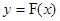 图象上任意不同的两点
图象上任意不同的两点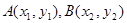 ,如果对于函数
,如果对于函数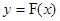 图象上的点
图象上的点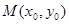 (其中
(其中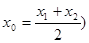 总能使得
总能使得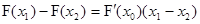 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数 是不是具备性质“
是不是具备性质“ ”,并说明理由.
”,并说明理由.
 =
=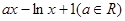 ,
,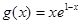 .
.(1)求函数
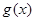 在区间
在区间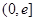 上的值域;
上的值域;(2)是否存在实数
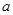 ,对任意给定的
,对任意给定的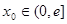 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的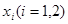 ,使得
,使得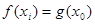 成立.若存在,求出
成立.若存在,求出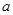 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.(3)给出如下定义:对于函数
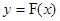 图象上任意不同的两点
图象上任意不同的两点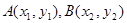 ,如果对于函数
,如果对于函数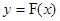 图象上的点
图象上的点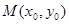 (其中
(其中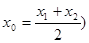 总能使得
总能使得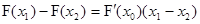 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数 是不是具备性质“
是不是具备性质“ ”,并说明理由.
”,并说明理由.(1)值域为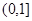 .(2)满足条件的
.(2)满足条件的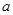 不存在. (3)函数
不存在. (3)函数 不具备性质“
不具备性质“ ”.
”.
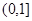 .(2)满足条件的
.(2)满足条件的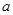 不存在. (3)函数
不存在. (3)函数 不具备性质“
不具备性质“ ”.
”. 本试题主要是考查了导数在研究函数中的运用。
(1)因为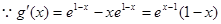 ,然后分析导数的正负,然后判定单调性得到值域。
,然后分析导数的正负,然后判定单调性得到值域。
(2)令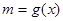 ,则由(1)可得
,则由(1)可得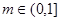 ,原问题等价于:对任意的
,原问题等价于:对任意的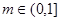
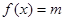 在
在 上总有两个不同的实根,故
上总有两个不同的实根,故 在
在 不可能是单调函数,对于参数a讨论得到结论。
不可能是单调函数,对于参数a讨论得到结论。
(3)结合导数的几何意义得到结论。
(1)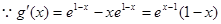 ,当
,当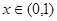 时,
时,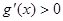 ,
,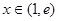 时,
时,
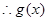 在区间
在区间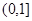 上单调递增,在区间
上单调递增,在区间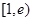 上单调递减,且
上单调递减,且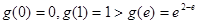 ,
,
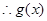 的值域为
的值域为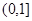 . ………………………….3分
. ………………………….3分
(2)令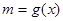 ,则由(1)可得
,则由(1)可得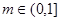 ,原问题等价于:对任意的
,原问题等价于:对任意的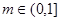
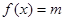 在
在 上总有两个不同的实根,故
上总有两个不同的实根,故 在
在 不可能是单调函数 ……5分
不可能是单调函数 ……5分

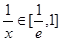
当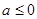 时,
时, 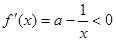 ,
, 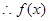 在区间
在区间 上递减,不合题意 ;
上递减,不合题意 ;
当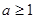 时,
时, 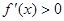 ,
, 在区间
在区间 上单调递增,不合题意;
上单调递增,不合题意;
当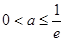 时,
时, 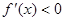 ,
, 在区间
在区间 上单调递减,不合题意;
上单调递减,不合题意;
当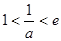 即
即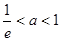 时,
时,  在区间
在区间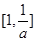 上单调递减;
上单调递减;  在区间
在区间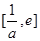 上单递增,由上可得
上单递增,由上可得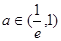 ,此时必有
,此时必有 的最小值小于等于0且
的最小值小于等于0且 的最大值大于等于1, 而由
的最大值大于等于1, 而由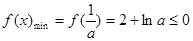 可得
可得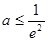 ,则
,则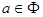 .
.
综上,满足条件的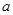 不存在.……………………………………………8分
不存在.……………………………………………8分
(3)设函数 具备性质“
具备性质“ ”,即在点
”,即在点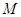 处地切线斜率等于
处地切线斜率等于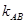 ,不妨设
,不妨设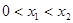 ,则
,则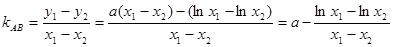 ,而
,而 在点
在点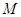 处的切线斜率为
处的切线斜率为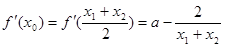 ,故有
,故有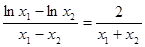 ……..10分
……..10分
即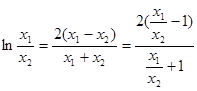 ,令
,令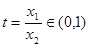 ,则上式化为
,则上式化为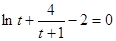 ,
,
令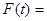
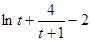 ,则由
,则由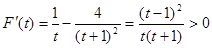 可得
可得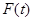 在
在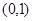 上单调递增,故
上单调递增,故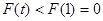 ,即方程
,即方程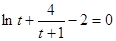 无解,所以函数
无解,所以函数 不具备性质“
不具备性质“ ”.……..14分
”.……..14分
(1)因为
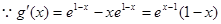 ,然后分析导数的正负,然后判定单调性得到值域。
,然后分析导数的正负,然后判定单调性得到值域。(2)令
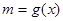 ,则由(1)可得
,则由(1)可得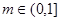 ,原问题等价于:对任意的
,原问题等价于:对任意的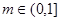
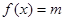 在
在 上总有两个不同的实根,故
上总有两个不同的实根,故 在
在 不可能是单调函数,对于参数a讨论得到结论。
不可能是单调函数,对于参数a讨论得到结论。(3)结合导数的几何意义得到结论。
(1)
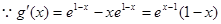 ,当
,当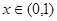 时,
时,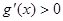 ,
,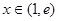 时,
时,
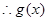 在区间
在区间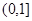 上单调递增,在区间
上单调递增,在区间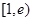 上单调递减,且
上单调递减,且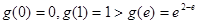 ,
,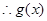 的值域为
的值域为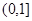 . ………………………….3分
. ………………………….3分(2)令
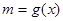 ,则由(1)可得
,则由(1)可得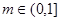 ,原问题等价于:对任意的
,原问题等价于:对任意的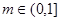
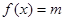 在
在 上总有两个不同的实根,故
上总有两个不同的实根,故 在
在 不可能是单调函数 ……5分
不可能是单调函数 ……5分
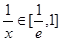
当
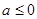 时,
时, 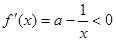 ,
, 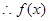 在区间
在区间 上递减,不合题意 ;
上递减,不合题意 ;当
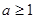 时,
时, 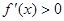 ,
, 在区间
在区间 上单调递增,不合题意;
上单调递增,不合题意;当
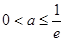 时,
时, 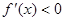 ,
, 在区间
在区间 上单调递减,不合题意;
上单调递减,不合题意;当
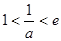 即
即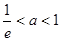 时,
时,  在区间
在区间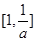 上单调递减;
上单调递减;  在区间
在区间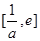 上单递增,由上可得
上单递增,由上可得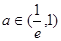 ,此时必有
,此时必有 的最小值小于等于0且
的最小值小于等于0且 的最大值大于等于1, 而由
的最大值大于等于1, 而由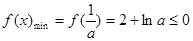 可得
可得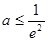 ,则
,则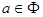 .
.综上,满足条件的
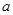 不存在.……………………………………………8分
不存在.……………………………………………8分(3)设函数
 具备性质“
具备性质“ ”,即在点
”,即在点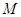 处地切线斜率等于
处地切线斜率等于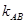 ,不妨设
,不妨设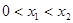 ,则
,则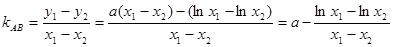 ,而
,而 在点
在点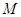 处的切线斜率为
处的切线斜率为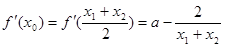 ,故有
,故有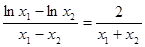 ……..10分
……..10分即
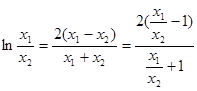 ,令
,令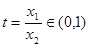 ,则上式化为
,则上式化为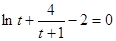 ,
,令
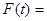
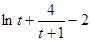 ,则由
,则由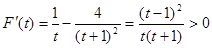 可得
可得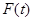 在
在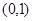 上单调递增,故
上单调递增,故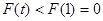 ,即方程
,即方程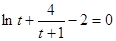 无解,所以函数
无解,所以函数 不具备性质“
不具备性质“ ”.……..14分
”.……..14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
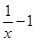
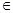 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;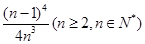 ∈N*).
∈N*).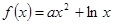 .
.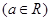
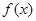 的单调性;
的单调性;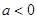 ,若函数
,若函数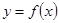 的图象总在直线
的图象总在直线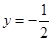 的下方,求
的下方,求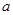 的取值范围;
的取值范围;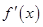 为函数
为函数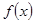 的导函数.若
的导函数.若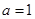 ,试问:在区间
,试问:在区间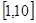 上是否存在
上是否存在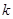 (
(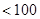 )个正数
)个正数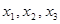 …
…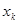 ,使得
,使得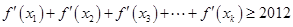 成立?请证明你的结论.
成立?请证明你的结论.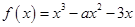
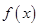 在
在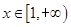 上是增函数,求实数
上是增函数,求实数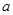 的取值范围;
的取值范围;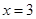 是
是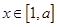 上的最小值和最大值.
上的最小值和最大值.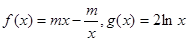 .
.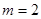 时,求曲线
时,求曲线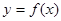 在点
在点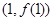 处的切线方程;
处的切线方程;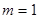 时,判断方程
时,判断方程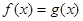 实根个数.
实根个数.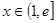 时,不等式
时,不等式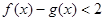 恒成立,求实数
恒成立,求实数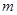 的取值范围.
的取值范围. 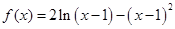 .
.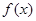 的单调递增区间;
的单调递增区间;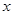 的方程
的方程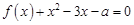 在区间
在区间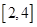 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数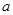 的取值范围.
的取值范围. 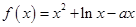 在(0,1)上是增函数.(1)求
在(0,1)上是增函数.(1)求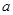 的取值范围;
的取值范围;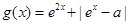 (
(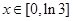 ),试求函数
),试求函数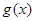 的最小值.
的最小值.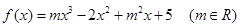 且
且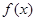 在
在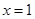 处取得极小值.
处取得极小值.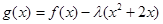 在
在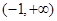 上是增函数,求实数
上是增函数,求实数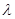 的取值范围。
的取值范围。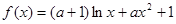 .
.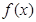 的单调性;
的单调性;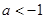 .如果对任意
.如果对任意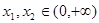 ,
,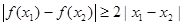 ,求
,求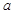 的取值范围.
的取值范围.