题目内容
已知函数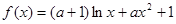 .
.
(Ⅰ)讨论函数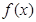 的单调性;
的单调性;
(Ⅱ)设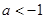 .如果对任意
.如果对任意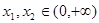 ,
,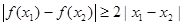 ,求
,求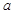 的取值范围.
的取值范围.
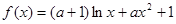 .
.(Ⅰ)讨论函数
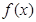 的单调性;
的单调性;(Ⅱ)设
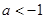 .如果对任意
.如果对任意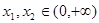 ,
,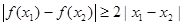 ,求
,求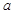 的取值范围.
的取值范围.(Ⅰ)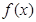 在
在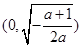 单调增加,在
单调增加,在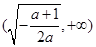 单调减少
单调减少
(Ⅱ)(-∞,-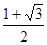 ].
].
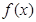 在
在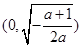 单调增加,在
单调增加,在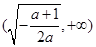 单调减少
单调减少(Ⅱ)(-∞,-
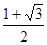 ].
].(1)先确定函数的定义域然后求导数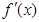 ,在函数的定义域内解不等式
,在函数的定义域内解不等式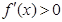 和
和 ,求出单调区间.(2)根据第一问的单调性先对|f(x1)-f(x2)|≥2|x1-x2|进行化简整理,转化成研究g(x)=f(x)+2x在(0,+∞)单调减函数,再利用参数分离法求出a的范围.
,求出单调区间.(2)根据第一问的单调性先对|f(x1)-f(x2)|≥2|x1-x2|进行化简整理,转化成研究g(x)=f(x)+2x在(0,+∞)单调减函数,再利用参数分离法求出a的范围.
解:(Ⅰ)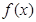 的定义域为(0,+∞).
的定义域为(0,+∞). 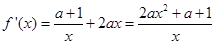 .
.
当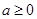 时,
时,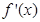 >0,故
>0,故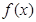 在(0,+∞)单调增加;
在(0,+∞)单调增加;
当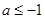 时,
时,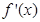 <0,故
<0,故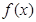 在(0,+∞)单调减少;
在(0,+∞)单调减少;
当-1<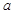 <0时,令
<0时,令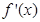 =0,解得
=0,解得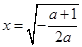 .
.
则当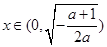 时,
时,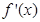 >0;
>0;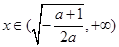 时,
时,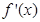 <0.
<0.
故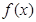 在
在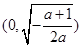 单调增加,在
单调增加,在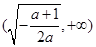 单调减少.
单调减少.
(Ⅱ)不妨假设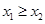 ,而
,而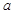 <-1,由(Ⅰ)知在(0,+∞)单调减少,从而
<-1,由(Ⅰ)知在(0,+∞)单调减少,从而
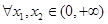 ,
, 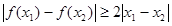
等价于
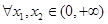 ,
, 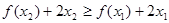 ①
①
令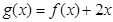 ,则
,则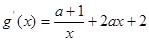
①等价于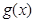 在(0,+∞)单调减少,即
在(0,+∞)单调减少,即

从而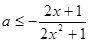 ,令
,令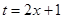 ,
,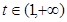 ,则
,则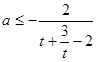
故a的取值范围为(-∞,-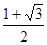 ].
].
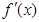 ,在函数的定义域内解不等式
,在函数的定义域内解不等式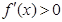 和
和 ,求出单调区间.(2)根据第一问的单调性先对|f(x1)-f(x2)|≥2|x1-x2|进行化简整理,转化成研究g(x)=f(x)+2x在(0,+∞)单调减函数,再利用参数分离法求出a的范围.
,求出单调区间.(2)根据第一问的单调性先对|f(x1)-f(x2)|≥2|x1-x2|进行化简整理,转化成研究g(x)=f(x)+2x在(0,+∞)单调减函数,再利用参数分离法求出a的范围.解:(Ⅰ)
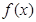 的定义域为(0,+∞).
的定义域为(0,+∞). 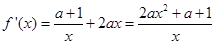 .
.当
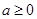 时,
时,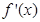 >0,故
>0,故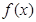 在(0,+∞)单调增加;
在(0,+∞)单调增加;当
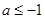 时,
时,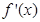 <0,故
<0,故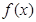 在(0,+∞)单调减少;
在(0,+∞)单调减少;当-1<
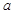 <0时,令
<0时,令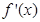 =0,解得
=0,解得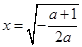 .
.则当
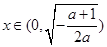 时,
时,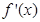 >0;
>0;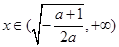 时,
时,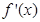 <0.
<0.故
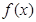 在
在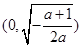 单调增加,在
单调增加,在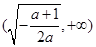 单调减少.
单调减少.(Ⅱ)不妨假设
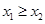 ,而
,而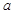 <-1,由(Ⅰ)知在(0,+∞)单调减少,从而
<-1,由(Ⅰ)知在(0,+∞)单调减少,从而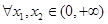 ,
, 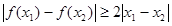
等价于
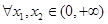 ,
, 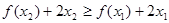 ①
①令
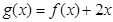 ,则
,则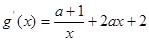
①等价于
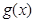 在(0,+∞)单调减少,即
在(0,+∞)单调减少,即
从而
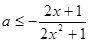 ,令
,令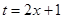 ,
,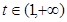 ,则
,则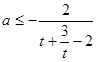
故a的取值范围为(-∞,-
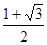 ].
].
练习册系列答案
相关题目
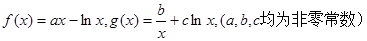 .
.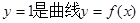 的切线,函数
的切线,函数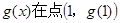 处取得极值1,求
处取得极值1,求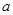 ,
,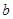 ,
,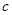 的值;
的值; 证明:
证明: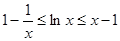 ;
; 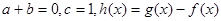 ,且函数
,且函数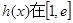 上单调递增,
上单调递增,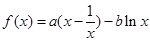 (
(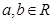 ),
),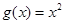 .
.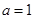 ,曲线
,曲线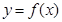 在点
在点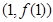 处的切线与
处的切线与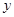 轴垂直,求
轴垂直,求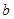 的值;
的值;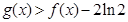 ;
;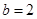 ,试探究函数
,试探究函数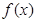 与
与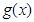 的图象在其公共点处是否存在公切线,若存在,研究
的图象在其公共点处是否存在公切线,若存在,研究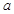 值的个数;若不存在,请说明理由.
值的个数;若不存在,请说明理由.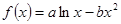 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为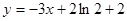 .
.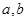 的值;
的值;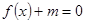 在
在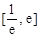 内有两个不等实根,求
内有两个不等实根,求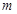 的取值范围(其中
的取值范围(其中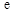 为自然对数的底);
为自然对数的底);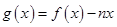 ,如果
,如果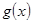 图象与
图象与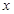 轴交于
轴交于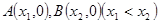 ,AB中点为
,AB中点为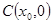 ,求证:
,求证: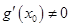 .
. =
=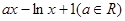 ,
,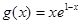 .
.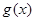 在区间
在区间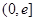 上的值域;
上的值域;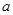 ,对任意给定的
,对任意给定的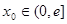 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的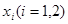 ,使得
,使得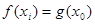 成立.若存在,求出
成立.若存在,求出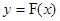 图象上任意不同的两点
图象上任意不同的两点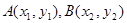 ,如果对于函数
,如果对于函数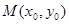 (其中
(其中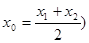 总能使得
总能使得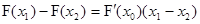 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数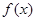 在
在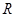 上可导,其导函数
上可导,其导函数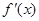 ,且函数
,且函数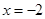 处取得极小值,
处取得极小值,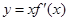 的图象可能是( )
的图象可能是( )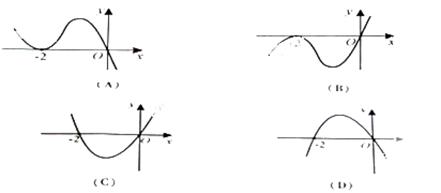
 的定义域为(0,
的定义域为(0,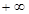 ),且
),且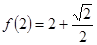 ,设点P是函数图象上的任意一点,过点P分别作直线
,设点P是函数图象上的任意一点,过点P分别作直线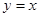 和
和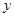 轴的垂线,垂足分别为M、N.
轴的垂线,垂足分别为M、N.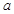 的值;
的值;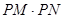 是否为定值?若是,则求出该定值,若不是,请说明理由;
是否为定值?若是,则求出该定值,若不是,请说明理由;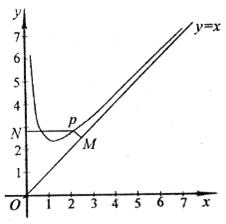
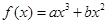 的图像经过点
的图像经过点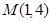 ,曲线在点
,曲线在点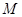 处的切线恰好与直线
处的切线恰好与直线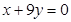 垂直.
垂直.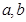 的值;
的值;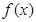 在区间
在区间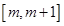 上单调递增,求实数
上单调递增,求实数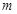 的取值范围.
的取值范围.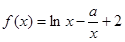 。
。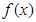 的单调区间;
的单调区间;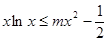 在
在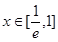 上恒成立,求
上恒成立,求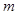 的取值范围。
的取值范围。