题目内容
(本题满分12分)
已知函数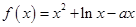 在(0,1)上是增函数.(1)求
在(0,1)上是增函数.(1)求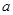 的取值范围;
的取值范围;
(2)设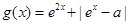 (
(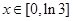 ),试求函数
),试求函数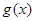 的最小值.
的最小值.
已知函数
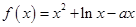 在(0,1)上是增函数.(1)求
在(0,1)上是增函数.(1)求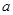 的取值范围;
的取值范围;(2)设
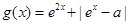 (
(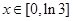 ),试求函数
),试求函数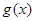 的最小值.
的最小值.(1)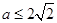 ;(2)当
;(2)当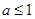 时,
时,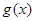 的最小值为
的最小值为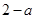 ;当
;当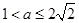 时,
时,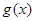 的最小值为
的最小值为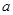 。
。
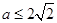 ;(2)当
;(2)当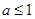 时,
时,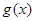 的最小值为
的最小值为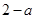 ;当
;当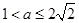 时,
时,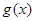 的最小值为
的最小值为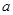 。
。(1)本小题实质是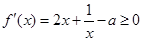 在
在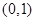 上恒成立,即转化为
上恒成立,即转化为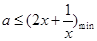 .
.
(2) 设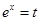 ,则
,则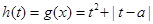 ,由
,由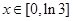 ,得
,得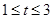 .
.
根据(1)中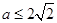 ,因此要分
,因此要分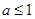 和
和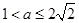 两种情况研究h(t)的最小值.
两种情况研究h(t)的最小值.
选做题(从22、23、24中选择其中一题作答.满分10分)
(1)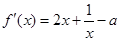 ……2分 ∵
……2分 ∵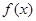 在(0,1)上是增函数
在(0,1)上是增函数
∴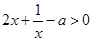 在(0,1)上恒成立,即
在(0,1)上恒成立,即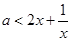 在(0,1)上恒成立
在(0,1)上恒成立
∵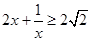 (当且仅当
(当且仅当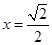 时取等号)……4分
时取等号)……4分
∴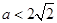 当
当 时,
时,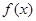 在(0,1)上也是增函数
在(0,1)上也是增函数
∴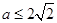 ……………………………………… 6分
……………………………………… 6分
(2)设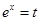 ,则
,则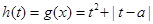
∵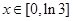 ∴
∴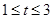
当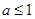 时,
时,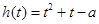 在区间
在区间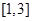 上是增函数
上是增函数
∴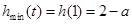 ……………………………8分
……………………………8分
当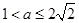 时,
时, 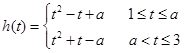 在区间
在区间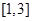 上是增函数
上是增函数
∴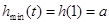 ……………………………10分
……………………………10分
综上:当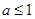 时,
时,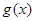 的最小值为
的最小值为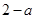 ;
;
当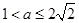 时,
时,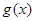 的最小值为
的最小值为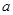 …………………………… 12分
…………………………… 12分
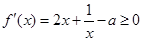 在
在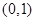 上恒成立,即转化为
上恒成立,即转化为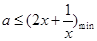 .
.(2) 设
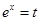 ,则
,则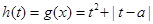 ,由
,由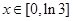 ,得
,得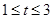 .
.根据(1)中
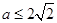 ,因此要分
,因此要分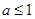 和
和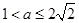 两种情况研究h(t)的最小值.
两种情况研究h(t)的最小值.选做题(从22、23、24中选择其中一题作答.满分10分)
(1)
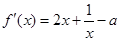 ……2分 ∵
……2分 ∵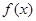 在(0,1)上是增函数
在(0,1)上是增函数∴
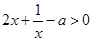 在(0,1)上恒成立,即
在(0,1)上恒成立,即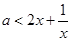 在(0,1)上恒成立
在(0,1)上恒成立∵
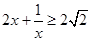 (当且仅当
(当且仅当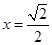 时取等号)……4分
时取等号)……4分∴
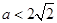 当
当 时,
时,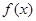 在(0,1)上也是增函数
在(0,1)上也是增函数∴
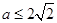 ……………………………………… 6分
……………………………………… 6分(2)设
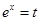 ,则
,则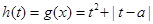
∵
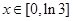 ∴
∴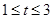
当
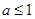 时,
时,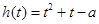 在区间
在区间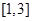 上是增函数
上是增函数∴
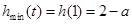 ……………………………8分
……………………………8分当
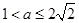 时,
时, 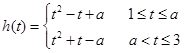 在区间
在区间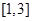 上是增函数
上是增函数∴
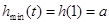 ……………………………10分
……………………………10分综上:当
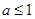 时,
时,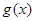 的最小值为
的最小值为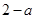 ;
;当
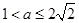 时,
时,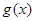 的最小值为
的最小值为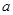 …………………………… 12分
…………………………… 12分
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
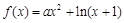 .
.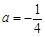 时,求函数
时,求函数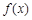 的单调区间;
的单调区间;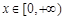 时,函数
时,函数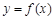 图象上的点都在
图象上的点都在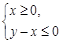 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.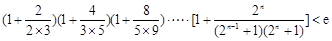 (其中
(其中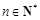 ,e是自然对数的底数).
,e是自然对数的底数).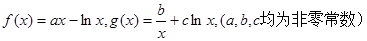 .
.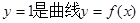 的切线,函数
的切线,函数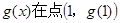 处取得极值1,求
处取得极值1,求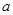 ,
,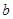 ,
,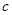 的值;
的值;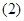 证明:
证明: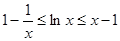 ;
; 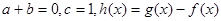 ,且函数
,且函数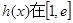 上单调递增,
上单调递增,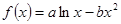 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为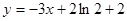 .
.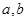 的值;
的值;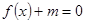 在
在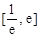 内有两个不等实根,求
内有两个不等实根,求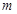 的取值范围(其中
的取值范围(其中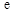 为自然对数的底);
为自然对数的底);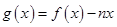 ,如果
,如果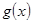 图象与
图象与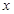 轴交于
轴交于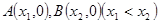 ,AB中点为
,AB中点为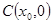 ,求证:
,求证: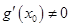 .
.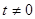 ,点P(
,点P(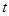 ,0)是函数
,0)是函数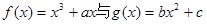 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.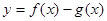 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求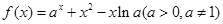 .
.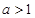 时,求证:函数
时,求证:函数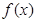 在
在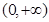 上单调递增;
上单调递增;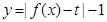 有三个零点,求
有三个零点,求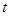 的值;
的值;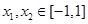 ,使得
,使得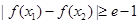 ,试求
,试求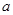 的取值范围。
的取值范围。 =
=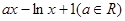 ,
,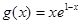 .
.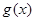 在区间
在区间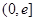 上的值域;
上的值域;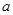 ,对任意给定的
,对任意给定的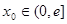 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的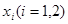 ,使得
,使得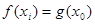 成立.若存在,求出
成立.若存在,求出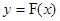 图象上任意不同的两点
图象上任意不同的两点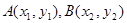 ,如果对于函数
,如果对于函数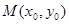 (其中
(其中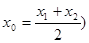 总能使得
总能使得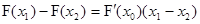 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数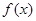 ,设其导函数
,设其导函数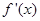 ,当
,当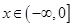 时,恒有
时,恒有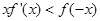 ,则满足
,则满足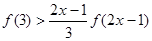 的实数
的实数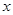 的取值范围是( )
的取值范围是( )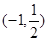
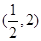
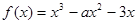 .
.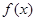 在
在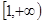 上是增函数,求实数
上是增函数,求实数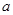 的取值范围;
的取值范围;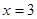 是
是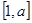 上的最小值和最大值.
上的最小值和最大值.