题目内容
(本题满分14分)
已知函数f(x)=lnx+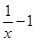
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m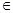 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n>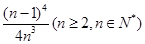 ∈N*).
∈N*).
已知函数f(x)=lnx+
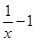
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m
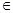 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n>
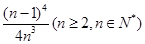 ∈N*).
∈N*).(Ⅰ)函数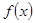 的单调递减区间是
的单调递减区间是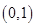 .
.
(Ⅱ)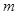 的取值范围是
的取值范围是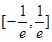 .
.
(Ⅲ)见解析。
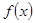 的单调递减区间是
的单调递减区间是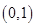 .
.(Ⅱ)
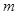 的取值范围是
的取值范围是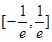 .
.(Ⅲ)见解析。
试题分析:(Ⅰ)
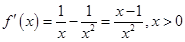 .
.令
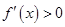 ,得
,得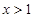 ,因此函数
,因此函数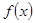 的单调递增区间是
的单调递增区间是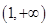 .
.令
 ,得
,得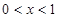 ,因此函数
,因此函数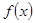 的单调递减区间是
的单调递减区间是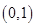 .…………(4分)
.…………(4分)(Ⅱ)依题意,
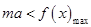 .
.由(Ⅰ)知,
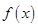 在
在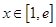 上是增函数,
上是增函数,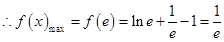 .
.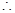
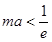 ,即
,即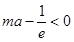 对于任意的
对于任意的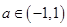 恒成立.
恒成立.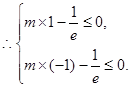 解得
解得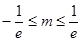 .
.所以,
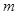 的取值范围是
的取值范围是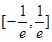 . …………………………(8分)
. …………………………(8分)(Ⅲ)由(Ⅰ)
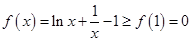 ,
,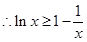 ,
,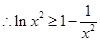 .
.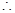
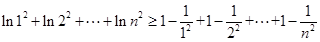 .
.即
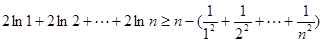 .
.又,
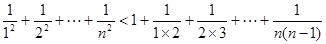
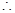
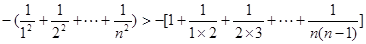
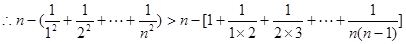
 .
.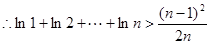 .
.由柯西不等式,
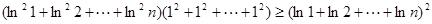 .
.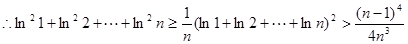 .
. . ……………………(14分)
. ……………………(14分)点评:较难题,利用导数求函数单调区间的方法,解题时注意函数的定义域,避免出错

练习册系列答案
相关题目
 的图象是连续不断的曲线,且有如下的对应值表
的图象是连续不断的曲线,且有如下的对应值表

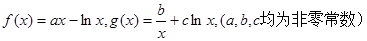 .
.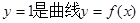 的切线,函数
的切线,函数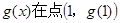 处取得极值1,求
处取得极值1,求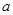 ,
,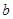 ,
,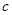 的值;
的值;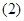 证明:
证明: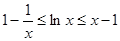 ;
; 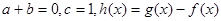 ,且函数
,且函数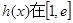 上单调递增,
上单调递增, .
. 时,判断f(x)在定义域上的单调性;
时,判断f(x)在定义域上的单调性; ,求
,求 的值.
的值.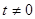 ,点P(
,点P(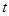 ,0)是函数
,0)是函数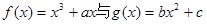 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.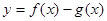 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求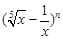 的展开式中,第4项是常数项,则
的展开式中,第4项是常数项,则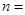
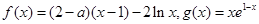 ,(
,(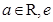 为自然对数的底数)。
为自然对数的底数)。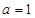 时,求函数
时,求函数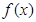 在区间
在区间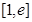 上的最大值和最小值;
上的最大值和最小值; 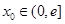 ,在
,在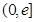 上总存在两个不同的
上总存在两个不同的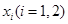 ,使得
,使得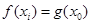 成立,求
成立,求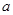 的取值范围。
的取值范围。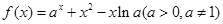 .
.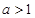 时,求证:函数
时,求证:函数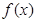 在
在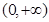 上单调递增;
上单调递增;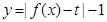 有三个零点,求
有三个零点,求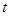 的值;
的值;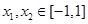 ,使得
,使得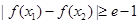 ,试求
,试求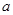 的取值范围。
的取值范围。 =
=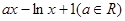 ,
,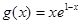 .
.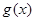 在区间
在区间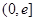 上的值域;
上的值域;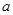 ,对任意给定的
,对任意给定的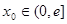 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的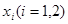 ,使得
,使得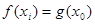 成立.若存在,求出
成立.若存在,求出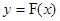 图象上任意不同的两点
图象上任意不同的两点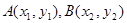 ,如果对于函数
,如果对于函数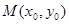 (其中
(其中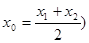 总能使得
总能使得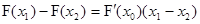 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数