题目内容
已知数列{an}满足a1=1,an=an-12-1(n>1),写出它的前5项.
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:根据an=
-1(n>1),写出它的前5项即可
| a | 2 n-1 |
解答:
解:∵a1=1,an=
-1
∴a2=a12-1=0,
a3=a22-1=-1,
a4=a32-1=0,
a5=a42-1=-1.
| a | 2 n-1 |
∴a2=a12-1=0,
a3=a22-1=-1,
a4=a32-1=0,
a5=a42-1=-1.
点评:本题考查数列的概念及数列的递推公式,属于基础题

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知函数f(x)=
其中a∈R,若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的最大值为( )
|
| A、-1 | B、-2 | C、-4 | D、-3 |
函数f(x)=lnx+
x的零点所在的区间是( )
| 1 |
| 3 |
| A、(1,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(-1,0) |
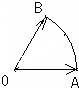 给定两个长度为1的平面向量
给定两个长度为1的平面向量