题目内容
在△ABC中，a，b，c分别是角A，B，C的对边，且sin2C+
cos（A+B）=0．
（1）若a=4，c=
，求b的长；
（2）若C＞A，A=60°，AB=5，求
•
+
•
+
•
的值．
| 3 |
（1）若a=4，c=
| 13 |
（2）若C＞A，A=60°，AB=5，求
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
考点：平面向量数量积的运算,余弦定理
专题：平面向量及应用
分析：由已知数据可得cosC=0或sinC=
，（1）由条件可得sinC=
，C=60°，由余弦定理可得；（2）由题意验证可得C=90°，由数量积的定义计算可得．
| ||
| 2 |
| ||
| 2 |
解答：
解：∵A+B+C=π，∴A+B=π-C，
∴sin2C+
cos(A+B)=2sinC•cosC+
cos(π-C)，
∴2sinCcosC-
cosC=cosC(2sinC-
)=0
∴cosC=0或sinC=
，
（1）∵a=4，c=
，∴c＜a，
∴C＜A，∴C为锐角，
∴sinC=
，此时C=60°
由余弦定理可得c2=a2+b2-2abcosC
代入数据可得13=16+b2-2•4•b•
，
化简可得b2-4b+3=0，
解得b=1或b=3，经检验均满足题意；
（2）∵C＞A，A=60°，∴C＞600，
若sinC=
，C=1200，A+C＞1800，不合题意
∴cosC=0，C=90°，
∴
•
+
•
+
•
=
•
+0+
•
=
•(
+
)=
•
=-
2=-25
∴sin2C+
| 3 |
| 3 |
∴2sinCcosC-
| 3 |
| 3 |
∴cosC=0或sinC=
| ||
| 2 |
（1）∵a=4，c=
| 13 |
∴C＜A，∴C为锐角，
∴sinC=
| ||
| 2 |
由余弦定理可得c2=a2+b2-2abcosC
代入数据可得13=16+b2-2•4•b•
| 1 |
| 2 |
化简可得b2-4b+3=0，
解得b=1或b=3，经检验均满足题意；
（2）∵C＞A，A=60°，∴C＞600，
若sinC=
| ||
| 2 |
∴cosC=0，C=90°，
∴
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
| AB |
| BC |
| CA |
| AB |
=
| AB |
| BC |
| CA |
| AB |
| BA |
| AB |
点评：本题考查平面向量的数量积，涉及三角函数和解三角形，属中档题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
直线y=5，与y=-1在区间[0，
]上截曲线y=Asinωx+B（A＞0，B＞0，ω＞0）所得弦长相等且不为零，则下列描述正确的是（ ）
| 2π |
| ω |
A、A≤
| ||||
| B、A≤3，B=2 | ||||
C、A＞
| ||||
| D、A＞3，B=2 |
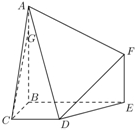如图，多面体ABCDEF中，BA、BC、BE两两垂直，且AB∥EF，CD∥BE，AB=BE=2，BC=CD=EF=1．
如图，AB，CD均为圆O的直径，CE⊥圆O所在的平面，BF∥CE，求证：
如图，在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥平面ABCD，PA=AB，∠ABC=60°，E、F分别是PB，CD的中点．