题目内容
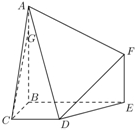 如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.(Ⅰ)若点G在线段AB上,且BG=3GA,求证:CG∥平面ADF;
(Ⅱ)求证:平面ABD⊥平面DEF.
(Ⅲ)求直线DF与平面ABEF所成的角的正弦值.
考点:平面与平面垂直的判定,直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)分别取AB、AF的中点M、H,连结MF,GH,DH,由已知条件推导出四边形CDHG是平行四边形,由此能证明CG∥平面ADF.
(II)由已知条件推导出BD⊥DE,从而得到BA⊥面BCDE,进而得到BA⊥DE,由此能证明DE⊥平面ABD,从而得到平面DEF⊥平面ABD.
(Ⅲ)取BE的中点O,连接OF,由已知条件推导出∠DFO是直线DF与平面ABEF所成的角,由此能求出直线DF与平面ABEF所成的角的正弦值.
(II)由已知条件推导出BD⊥DE,从而得到BA⊥面BCDE,进而得到BA⊥DE,由此能证明DE⊥平面ABD,从而得到平面DEF⊥平面ABD.
(Ⅲ)取BE的中点O,连接OF,由已知条件推导出∠DFO是直线DF与平面ABEF所成的角,由此能求出直线DF与平面ABEF所成的角的正弦值.
解答:
(Ⅰ)证明:分别取AB、AF的中点M、H,连结MF,GH,DH,
有AG=GM,MF
BE.
∵AH=HF,∴GH
MF,…(1分)
又∵CD
BE,BE
MF,∴CD
GH,
∴四边形CDHG是平行四边形,∴CG
DH,…(3分)
又∵CG不包含于平面ADF,DH?平面ADF,
∴CG∥平面ADF.…(4分)
(II)证明:在△BDE中,BD=
,DE=
,BE=2,
∴BD2+DE2=BE2,∴BD⊥DE,…(6分)
又∵BD⊥BC,BA⊥BE,BC∩BE=B,
∴BA⊥面BCDE,∴BA⊥DE,…(8分)
又∵AB∩BD=B,
∴DE⊥平面ABD,又∵DE?平面DEF,
∴平面DEF⊥平面ABD.…(9分)
(Ⅲ)解:取BE的中点O,连接OF,
∵BD=DE,∴OD⊥BE,
又∵AB⊥底面BCDE,∴AB⊥OD,
AB∩BE=B,∴OD⊥面ABEF,
∴OF为DF在面ABEF内的射影,∴∠DFO是直线DF与平面ABEF所成的角,…(11分)
在Rt△DFO中,DO=1,DF=
,
∴sin∠DFO=
,
∴直线DF与平面ABEF所成的角的正弦值为
.…(13分)
有AG=GM,MF
| ∥ |
. |
∵AH=HF,∴GH
| ∥ |
. |
| 1 |
| 2 |
又∵CD
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| ∥ |
. |
∴四边形CDHG是平行四边形,∴CG
| ∥ |
. |
又∵CG不包含于平面ADF,DH?平面ADF,
∴CG∥平面ADF.…(4分)
(II)证明:在△BDE中,BD=
| 2 |
| 2 |
∴BD2+DE2=BE2,∴BD⊥DE,…(6分)
又∵BD⊥BC,BA⊥BE,BC∩BE=B,
∴BA⊥面BCDE,∴BA⊥DE,…(8分)
又∵AB∩BD=B,
∴DE⊥平面ABD,又∵DE?平面DEF,
∴平面DEF⊥平面ABD.…(9分)
(Ⅲ)解:取BE的中点O,连接OF,
∵BD=DE,∴OD⊥BE,
又∵AB⊥底面BCDE,∴AB⊥OD,
AB∩BE=B,∴OD⊥面ABEF,
∴OF为DF在面ABEF内的射影,∴∠DFO是直线DF与平面ABEF所成的角,…(11分)
在Rt△DFO中,DO=1,DF=
| 3 |
∴sin∠DFO=
| ||
| 3 |
∴直线DF与平面ABEF所成的角的正弦值为
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
若k>1,a>0,则k2a2+
取得最小值时,a的值为( )
| 16 |
| (k-1)a2 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知{an}为等比数列,a5+a8=2,a6•a7=-8,则a2+a11=( )
| A、5 | B、7 | C、-7 | D、-5 |
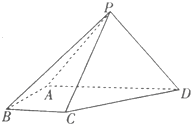 如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2
如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2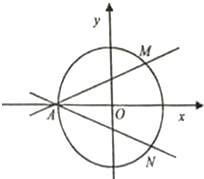 如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.