题目内容
已知双曲线C:
-
=1离心率是
,过点(
,1),且右支上的弦AB过右焦点F.
(1)求双曲线C的方程;
(2)求弦AB的中点M的轨迹E的方程;
(3)是否存在以AB为直径的圆过原点O?,若存在,求出直线AB的斜率k的值.若不存在,则说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
(1)求双曲线C的方程;
(2)求弦AB的中点M的轨迹E的方程;
(3)是否存在以AB为直径的圆过原点O?,若存在,求出直线AB的斜率k的值.若不存在,则说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件得
,由此能求出双曲线C的方程.
(2)设A(x1,y1),B(x2,y2),M(x,y),利用点差法能示出弦AB的中点M的轨迹E的方程.
(3)假设存在以AB为直径的圆过原点O,设A(x1,y1),B(x2,y2),直线AB:y=k(x-2),由
,得(1-k2)x2+4k2x-4k2-2=0,由x1x2+y1y2=0,得k2+1=0无解,故这样的圆不存在.
|
(2)设A(x1,y1),B(x2,y2),M(x,y),利用点差法能示出弦AB的中点M的轨迹E的方程.
(3)假设存在以AB为直径的圆过原点O,设A(x1,y1),B(x2,y2),直线AB:y=k(x-2),由
|
解答:
解:(1)∵双曲线C:
-
=1离心率是
,过点(
,1),
∴
,解得a=
,b=
,c=2,
∴双曲线C的方程x2-y2=2.
(2)∵右支上的弦AB过右焦点F(2,0),
∴设A(x1,y1),B(x2,y2),M(x,y),
∵弦AB的中点M,∴x1+x2=2x,y1+y2=2y,
把A,B分别代入双曲线C,得
,
两式相减,得2x(x1-x2)-2y(y1-y2)=0,
∴k=
=
,x≥2,
又∵直线AB过F(2,0),M(x,y),
∴k=
,∴
=
,
整理,得弦AB的中点M的轨迹E的方程:x2-2x-y2=0,x≥2.
(3)假设存在以AB为直径的圆过原点O,
设A(x1,y1),B(x2,y2),直线AB:y=k(x-2),
由
,得(1-k2)x2+4k2x-4k2-2=0,
△>0,x1+x2=
,x1x2=
,k2≠1,①
∵以AB为直径的圆过原点O,
∴x1x2+y1y2=0,
∴(1+k2)x1x2-2k2(x1+x2)+4k2=0,②
联立①②,得k2+1=0无解,
∴这样的圆不存在.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
∴
|
| 2 |
| 2 |
∴双曲线C的方程x2-y2=2.
(2)∵右支上的弦AB过右焦点F(2,0),
∴设A(x1,y1),B(x2,y2),M(x,y),
∵弦AB的中点M,∴x1+x2=2x,y1+y2=2y,
把A,B分别代入双曲线C,得
|
两式相减,得2x(x1-x2)-2y(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| x |
| y |
又∵直线AB过F(2,0),M(x,y),
∴k=
| y |
| x-2 |
| y |
| x-2 |
| x |
| y |
整理,得弦AB的中点M的轨迹E的方程:x2-2x-y2=0,x≥2.
(3)假设存在以AB为直径的圆过原点O,
设A(x1,y1),B(x2,y2),直线AB:y=k(x-2),
由
|
△>0,x1+x2=
| 4k2 |
| k2-1 |
| 4k2+2 |
| k2-1 |
∵以AB为直径的圆过原点O,
∴x1x2+y1y2=0,
∴(1+k2)x1x2-2k2(x1+x2)+4k2=0,②
联立①②,得k2+1=0无解,
∴这样的圆不存在.
点评:本题考查双曲线方程的求法,考查点的轨迹方程的求法,考查满足条件的圆是否存在的判断与求法,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
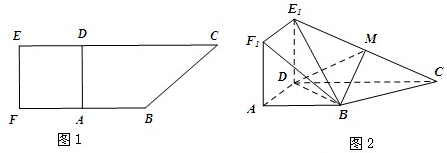

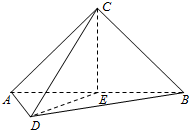 如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2
如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2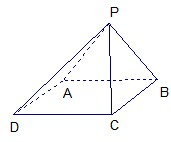 已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=