题目内容
已知抛物线C的一个焦点为F(
,0),准线方程为x=-
.
(1)写出抛物线C的方程;
(2)(此小题仅理科做)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆(x-3)2+y2=2的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?并求出|MN|的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
(1)写出抛物线C的方程;
(2)(此小题仅理科做)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆(x-3)2+y2=2的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?并求出|MN|的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意知抛物线方程为:y2=2x.
(2)当直线不垂直于x轴时,设方程为y=k(x-
),代入y2=2x,得k2x2-(k2+2)x+
=0,k≠0,设△AOB的重心为OG(x,y),由韦达定理得y2=
x-
.当直线垂直于x轴时,△AOB的重心G(
,0)也满足上述方程,由此能求出△AOB重心G的轨迹方程.
(3)已知圆的圆心为Q(3,0),半径r=
,当|PQ|2最小时,|MN|取最小值,由此能求出当P点坐标为P(2,±2)时,|MN|取最小值
.
(2)当直线不垂直于x轴时,设方程为y=k(x-
| 1 |
| 2 |
| k2 |
| 4 |
| 2 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
(3)已知圆的圆心为Q(3,0),半径r=
| 2 |
2
| ||
| 5 |
解答:
解:(1)∵抛物线C的一个焦点为F(
,0),准线方程为x=-
,
∴抛物线方程为:y2=2x.
(2)①当直线不垂直于x轴时,设方程为y=k(x-
),
代入y2=2x,得k2x2-(k2+2)x+
=0,k≠0,
设A(x1,y1),B(x2,y2),则x1+x2=
,y1+y2=k(x1+x2-1)=
,
设△AOB的重心为OG(x,y),
则
,
消去y,得y2=
x-
.
②当直线垂直于x轴时,A(
,1),B(
,-1),
△AOB的重心G(
,0)也满足上述方程.
综合①②,得所求的轨迹方程为y2=
x-
.
(3)已知圆的圆心为Q(3,0),半径r=
,
根据圆的性质有:|MN|=2•
=2r
=2
•
,
当|PQ|2最小时,|MN|取最小值.
设P(x0,y0),则y02=2x0,
|PQ|2=(x0-3)2+y02=x02-4x0+9=(x0-2)2+5,
∴当x0=2,y0=±2时,|PQ|2取最小值5,
故当P点坐标为P(2,±2)时,|MN|取最小值
.
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线方程为:y2=2x.
(2)①当直线不垂直于x轴时,设方程为y=k(x-
| 1 |
| 2 |
代入y2=2x,得k2x2-(k2+2)x+
| k2 |
| 4 |
设A(x1,y1),B(x2,y2),则x1+x2=
| k2+2 |
| k2 |
| 2 |
| k |
设△AOB的重心为OG(x,y),
则
|
消去y,得y2=
| 2 |
| 3 |
| 2 |
| 9 |
②当直线垂直于x轴时,A(
| 1 |
| 2 |
| 1 |
| 2 |
△AOB的重心G(
| 1 |
| 3 |
综合①②,得所求的轨迹方程为y2=
| 2 |
| 3 |
| 2 |
| 9 |
(3)已知圆的圆心为Q(3,0),半径r=
| 2 |
根据圆的性质有:|MN|=2•
| |MP||MQ| |
| |PQ| |
=2r
|
| 2 |
1-
|
当|PQ|2最小时,|MN|取最小值.
设P(x0,y0),则y02=2x0,
|PQ|2=(x0-3)2+y02=x02-4x0+9=(x0-2)2+5,
∴当x0=2,y0=±2时,|PQ|2取最小值5,
故当P点坐标为P(2,±2)时,|MN|取最小值
2
| ||
| 5 |
点评:本题考查抛物线方程的求法,考查点的轨迹方程的求法,考查线段长最小值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
经过点(-1,0),且与直线x+2y-3=0垂直的直线方程是( )
| A、2x-y+2=0 |
| B、2x+y+2=0 |
| C、2x-y-2=0 |
| D、x-2y+1=0 |
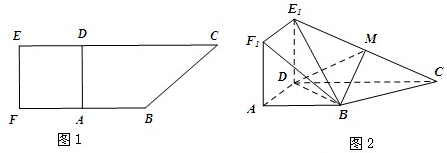
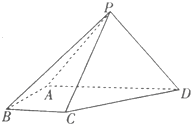 如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2
如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2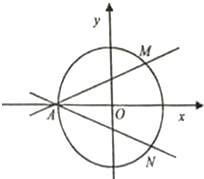 如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.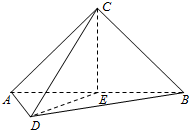 如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2
如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2