题目内容
设数列{an}的各项均为正数,它的前n项的和为Sn,点(an,Sn)在函数y=
x2+
x+
的图象上;数列{bn}满足b1=a1,bn+1(an+1-an)=bn.其中n∈N*.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
,求证:数列{cn}的前n项的和Tn>
(n∈N*).
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
| an |
| bn |
| 5 |
| 9 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)根据数列项和前n项和之间的关系即可求数列{an}和{bn}的通项公式;
(Ⅱ)求出cn=
是表达式,利用错位相减法求出数列{cn}的前n项的和,即可得到结论.
(Ⅱ)求出cn=
| an |
| bn |
解答:
解:(1)∵点(an,Sn)在函数y=
x2+
x+
的图象上,
∴Sn=
an2+
an+
,①
当n≥2时,Sn-1=
an-12+
an-1+
,②
①-②得:an=
(an2-an-12)+
(an-an-1),
即an+an-1=
(an+an-1)(an-an-1),
∵数列{an}的各项均为正数,
∴an-an-1=4(n≥2),
又a1=2,∴an=4n-2;
∵b1=a1,bn+1(an+1-an)=bn,
∴b1=2,
=
,∴bn=2•(
)n-1;
(2)∵cn=
=(2n-1)4n-1,
∴Tn=1+3•4+5•42+…+(2n-3)•4n-2+(2n-1)•4n-1,
4Tn=4+3•42+5•43+…+(2n-5)•4n-1+(2n-1)•4n,
两式相减得-3Tn=1+2(4+42+…+4n-1)-(2n-1)4n=-
-(2n-
)•4n<-
,
∴Tn>
.
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,Sn-1=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得:an=
| 1 |
| 8 |
| 1 |
| 2 |
即an+an-1=
| 1 |
| 4 |
∵数列{an}的各项均为正数,
∴an-an-1=4(n≥2),
又a1=2,∴an=4n-2;
∵b1=a1,bn+1(an+1-an)=bn,
∴b1=2,
| bn+1 |
| bn |
| 1 |
| 4 |
| 1 |
| 4 |
(2)∵cn=
| an |
| bn |
∴Tn=1+3•4+5•42+…+(2n-3)•4n-2+(2n-1)•4n-1,
4Tn=4+3•42+5•43+…+(2n-5)•4n-1+(2n-1)•4n,
两式相减得-3Tn=1+2(4+42+…+4n-1)-(2n-1)4n=-
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
∴Tn>
| 5 |
| 9 |
点评:本题主要考查数列通项公式的求解,以及数列求和,要求数列掌握错位相减法进行数列求和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
则y对x的线性回归方程为( )
| 父亲身高x(cm) | 174 | 175 | 176 | 176 | 179 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
| A、y=x-1 | ||
| B、y=x+1 | ||
C、y=88+
| ||
D、y=176+
|
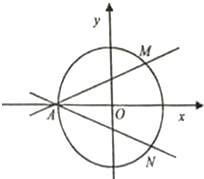 如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PA=AB=AD=2BC=2,∠BAD=θ,E是棱PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PA=AB=AD=2BC=2,∠BAD=θ,E是棱PD的中点.