题目内容
如图，AB，CD均为圆O的直径，CE⊥圆O所在的平面，BF∥CE，求证：（1）BC⊥平面ACE；
（2）面BDF∥平面ACE．
考点：直线与平面垂直的判定,平面与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（1）通过证明平面ACE内的直线CE与AC都垂直BC，可得BC⊥平面ACE；
（2）证明BD∥平面ACE、BF∥平面ACE，即可证明面BDF∥平面ACE．
（2）证明BD∥平面ACE、BF∥平面ACE，即可证明面BDF∥平面ACE．
解答：
证明：（1）因为CE⊥圆O所在的平面，BC?圆O所在的平面，
所以CE⊥BC，
因为AB为圆O的直径，点C在圆O上，所以AC⊥BC，
因为AC∩CE=C，AC，CE?平面ACE，
所以BC⊥平面ACE；
（2）由（1）AC⊥BC，又因为CD为圆O的直径，
所以BD⊥BC，
因为AC，BC，BD在同一平面内，所以AC∥BD．
因为BD?平面ACE，AC?平面ACE，所以BD∥平面ACE．
因为BF∥CE，同理可证BF∥平面ACE，
因为BD∩BF=B，BD，BF?平面BDF，
所以平面BDF∥平面ACE．
所以CE⊥BC，
因为AB为圆O的直径，点C在圆O上，所以AC⊥BC，
因为AC∩CE=C，AC，CE?平面ACE，
所以BC⊥平面ACE；
（2）由（1）AC⊥BC，又因为CD为圆O的直径，
所以BD⊥BC，
因为AC，BC，BD在同一平面内，所以AC∥BD．
因为BD?平面ACE，AC?平面ACE，所以BD∥平面ACE．
因为BF∥CE，同理可证BF∥平面ACE，
因为BD∩BF=B，BD，BF?平面BDF，
所以平面BDF∥平面ACE．
点评：本题考查平面与平面垂直的判定定理，直线与平面平行的判定定理的应用，考查空间想象能力以及逻辑推理能力．
练习册系列答案
相关题目
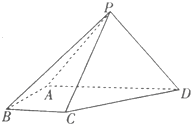如图在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，PA=PD=2，底面ABCD是直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2