题目内容
已知数列{an}的前n项和为Sn,且Sn=n2+2n.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{bn}中,b1=1,bn=2bn-1+1(n≥2),求{bn}的通项公式;
(Ⅲ)若cn=an(bn+1),求数列{cn}前几项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{bn}中,b1=1,bn=2bn-1+1(n≥2),求{bn}的通项公式;
(Ⅲ)若cn=an(bn+1),求数列{cn}前几项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由Sn=n2+2n,利用an=Sn-Sn-1(n≥2),再验证n=1,可求得an=2n+1;
(Ⅱ)易知,{bn+1}是2为首项,2为公比的等比数列,于是可求{bn}的通项公式;
(Ⅲ)cn=an(bn+1)=(2n+1)•2n,Tn=c1+c2+…+cn=3×2+5×22+7×23+…+(2n+1)•2n①,2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1②利用错位相减法即可求得Tn=(2n-1)×2n+1+2.
(Ⅱ)易知,{bn+1}是2为首项,2为公比的等比数列,于是可求{bn}的通项公式;
(Ⅲ)cn=an(bn+1)=(2n+1)•2n,Tn=c1+c2+…+cn=3×2+5×22+7×23+…+(2n+1)•2n①,2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1②利用错位相减法即可求得Tn=(2n-1)×2n+1+2.
解答:
解:(Ⅰ)∵Sn=n2+2n,
∴当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1,
当n=1时,a1=3,也符合上式,
∴an=2n+1;
(Ⅱ)由题意知bn=2bn-1+1,∴bn+1=2(bn-1+1)(n≥2),
∴
=2
∵b1+1=2,∴{bn+1}是2为首项,2为公比的等比数列,
∴bn+1=2•2n-1=2n.
∴bn=2n-1.
(Ⅲ)∵cn=an(bn+1)=(2n+1)•2n,
∴Tn=c1+c2+…+cn
=3×2+5×22+7×23+…+(2n+1)•2n,①
2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1,②
①-②得:-Tn=3×2+23+24+…+2n+1-(2n+1)•2n+1
=
-(2n+1)•2n+1
=2n+2-(2n+1)•2n+1-2,
∴Tn=(2n-1)×2n+1+2.
∴当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1,
当n=1时,a1=3,也符合上式,
∴an=2n+1;
(Ⅱ)由题意知bn=2bn-1+1,∴bn+1=2(bn-1+1)(n≥2),
∴
| bn+1 |
| bn-1+1 |
∵b1+1=2,∴{bn+1}是2为首项,2为公比的等比数列,
∴bn+1=2•2n-1=2n.
∴bn=2n-1.
(Ⅲ)∵cn=an(bn+1)=(2n+1)•2n,
∴Tn=c1+c2+…+cn
=3×2+5×22+7×23+…+(2n+1)•2n,①
2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1,②
①-②得:-Tn=3×2+23+24+…+2n+1-(2n+1)•2n+1
=
| 2(1-2n+1) |
| 1-2 |
=2n+2-(2n+1)•2n+1-2,
∴Tn=(2n-1)×2n+1+2.
点评:本题考查数列的求和,着重考查等差关系与等比关系的确定及通项公式的应用,突出考查错位相减法的应用,属于难题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知{an}为等比数列,a5+a8=2,a6•a7=-8,则a2+a11=( )
| A、5 | B、7 | C、-7 | D、-5 |
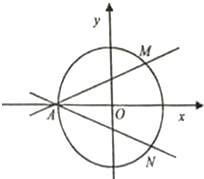 如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
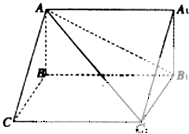 如图,在三棱柱ABC-A1B1C1中,已知AB=BC=1,CC1=2,AC1与平面BCC1B1所成角为30°,AB⊥平面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知AB=BC=1,CC1=2,AC1与平面BCC1B1所成角为30°,AB⊥平面BB1C1C.