题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)为偶函数,其图象上相邻的两个最低点间的距离为2π.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若将函数f(x)图象向右平移
个单位得到函数g(x)图象,若α∈[0,π],且g(α)=
,求α的值.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若将函数f(x)图象向右平移
| π |
| 3 |
| 1 |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)因为周期为2π,所以ω=1,又因为0≤φ≤π,f(x)为偶函数,可求得φ=
,从而可得f(x)的解析式;
(Ⅱ)依题意,可得cos(α-
)=
,继而可求得α=2kπ或α=2kπ+
(k∈Z),又α∈[0,π],从而可得答案.
| π |
| 2 |
(Ⅱ)依题意,可得cos(α-
| π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
解答:
解:(Ⅰ)因为周期为2π,所以ω=1,又因为0≤φ≤π,f(x)为偶函数,
所以φ=
,则f(x)=sin(x+
)=cos x.
(Ⅱ)由(Ⅰ)f(x)=cosx得:g(α)=cos(α-
)=
,α-
=2kπ±
,
故α=2kπ或α=2kπ+
(k∈Z),
α∈[0,π],
所以α=0或α=
.
所以φ=
| π |
| 2 |
| π |
| 2 |
(Ⅱ)由(Ⅰ)f(x)=cosx得:g(α)=cos(α-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
故α=2kπ或α=2kπ+
| 2π |
| 3 |
α∈[0,π],
所以α=0或α=
| 2π |
| 3 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查余弦函数的图象与性质,考查转化思想.

练习册系列答案
相关题目
4个人排成一排,甲不能站在两边,则不同的排法种数有( )种.
| A、12 | B、16 | C、8 | D、20 |
加工一种零件需要三道工序,其中只会第一道工序的有4人,只会第二道工序的有2人,只会第三道工序的有3人,现在从每道工序中各选一人加工这种零件,共有( )种不同的选派方法.
| A、9 | B、12 | C、24 | D、30 |
对于任意x∈R,同时满足条件f(x)=f(-x)和f(x-π)=f(x)的函数是( )
| A、f(x)=sinx |
| B、f(x)=sinxcosx |
| C、f(x)=cosx |
| D、f(x)=cos2x-sin2x |
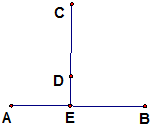 如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.
如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.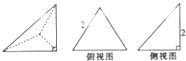 已知三棱锥的直观图及其俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图面积为( )
已知三棱锥的直观图及其俯视图与侧视图如图,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图面积为( )