题目内容
4个人排成一排,甲不能站在两边,则不同的排法种数有( )种.
| A、12 | B、16 | C、8 | D、20 |
考点:排列、组合及简单计数问题
专题:排列组合
分析:根据题意,假设4个人分别对应4个空位,甲甲不能站在两边,有2个位置可选;而其他3人对应其他3个位置,对其全排列,可得其排法数目,由分步计数原理计算可得答案.
解答:
解:假设4个人分别对应4个空位,甲甲不能站在两边,有2个位置可选;
则其他3人对应其他3个位置,有A33=6种情况,
则不同排列方法种数2×6=12种;
故选:A
则其他3人对应其他3个位置,有A33=6种情况,
则不同排列方法种数2×6=12种;
故选:A
点评:本题考查排列、组合的运用,一般要先处理特殊(受到限制的)元素.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),然后把图象向左平移
个单位,则所得图形对应的函数解析式为( )
| π |
| 8 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(
|
函数f(x)=x-3+log3x的零点所在的区间是( )
| A、(0,1) |
| B、(1,3) |
| C、(-∞,0) |
| D、(3,+∞) |
不等式(a2-1)x2-(a-1)x-1<0的解集为全体实数,则实数a的取值范围是( )
A、-
| ||
B、-
| ||
C、-
| ||
| D、a<-1或a>1 |
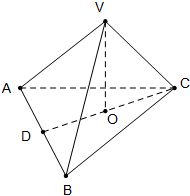 如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证:
如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证: