题目内容

已知点A（-2，0），B（2，0），∠APB=135°．
（1）求点P的轨迹方程；
（2）点C（2，4），在（1）的轨迹上求一点M，使得|CM|最小，并求其最小值．
考点：轨迹方程
专题：直线与圆
分析：（1）由题意结合正弦定理求出△ABP外接圆的直径及圆心坐标，得到P在x轴上方和下方的两个三角形的外接圆方程，得到以AB为弦的劣弧的轨迹得答案；
（2）画出图形，由图形可得M点为圆心和C的连线与圆的交点，求出直线方程，联立直线和圆锥曲线方程得答案．
解答： 解：（1）∵A（-2，0），B（2，0），
∴|AB|=4，在△ABP中，由
|AB|
sin∠APB
=
4
2
2
=4
2
，可知点P在过点A、B且直径为4
2
的圆上，
点P的轨迹为以AB为弦的劣弧（除A、B两点）．
且圆的圆心在y轴上，分别为（0，2）和（0，-2），
从而点P的轨迹方程为：x2+(y-2)2=8(2-2
2
≤y＜0)或x2+(y+2)2=8(0＜y≤2+2
2
)；
（2）如图，

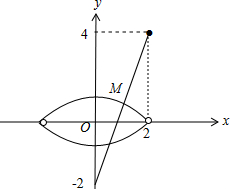
由图可知，使得|CM|最小的点M在x2+(y+2)2=8(0＜y≤2+2
2
)上，
而圆x2+(y+2)2=8(0＜y≤2+2
2
)的圆心为（0，-2），
C（2，4）到圆心的距离为
(2-0)2+(4+2)2
=2
10
．
圆的半径为2
2
，此时|FM|的最小值为2
10
-2
2
．
圆心与C的连线所在的方程为
y+2
4+2
=
x-0
2-0
，即y=3x-2．
联立
y=3x-2
x2+(y+2)2=8
，解得
x=
2
5
5
y=
6
5
-10
5
．
∴M（
2
5
5
，
6
5
-10
5
）．
点评：本题考查了轨迹方程的求法，考查了数形结合的解题思想方法，考查了数学转化思想方法，是中档题．
练习册系列答案
相关题目
下列命题为真命题的是
 
．（用序号表示即可）
①cos1＞cos2＞cos3；
②若an=an+3且an=n+3（n=1、2、3），则a2013＜a2014＜a2015；
③若e1、e2、e3分别为双曲线x2-
y2
3
=1、
x2
4
-
y2
3
=1、
x2
4
-y2=1的离心率，则e1＞e2＞e3；
④若x1＞x2＞x3，则lgx1＞lgx2＞lgx3．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）中，若以其焦点为圆心，半实轴长为半径的圆与渐近线相切，则其渐近线方程为
 
．
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半（纵坐标不变），然后把图象向左平移
π
8
个单位，则所得图形对应的函数解析式为（　　）
A、y=cos（
1
2
x+
π
4
）
B、y=cos（2x+
π
4
）
C、y=cos(
1
2
x+
π
8
)
D、y=cos（
1
2
x+
π
2
）
已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜
π
2
）相邻的最高点和最低点分别为（
π
6
，2），（
2π
3
，-2）．求函数表达式．
已知数列{an}满足a1=1，an+1=3an+4（n∈N*），数列{an}的通项公式
 
．
已知函数f（x）=sin（ωx+φ）（ω＞0，0≤φ≤π）为偶函数，其图象上相邻的两个最低点间的距离为2π．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若将函数f（x）图象向右平移
π
3
个单位得到函数g（x）图象，若α∈[0，π]，且g（α）=
1
2
，求α的值．
已知椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）和⊙C2：x2+y2=r2（r＞0）都经过点P（-1，0），且椭圆C1的离心率e=
2
2
，过点P作斜率为k1，k2的直线l1，l2分别交椭圆C1、⊙C2于点A，B，C，D，k1=λk2．
（1）求椭圆C1和⊙C2的方程；
（2）若直线BC恒过定点Q（1，0）求实数λ的值；
（3）当k1=
1
2
时，求△PAC面积的最大值．
已知函数f（x）=x2-2ax-1，在[0，2]]内的最大值为g（a）．
（Ⅰ）求g（a）的表达式；
（Ⅱ）求g（a）的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网