题目内容
直线L过点M（-2，1），与x，y轴分别交于A，B两点．
（1）若
=
，求直线L的方程；
（2）若
=2
，求直线L的方程；
（3）若|
|=2|
|，求直线L的方程．
（1）若
| AM |
| MB |
（2）若
| AM |
| MB |
（3）若|
| AM |
| MB |
考点：恒过定点的直线
专题：直线与圆
分析：（1）设出A，B的坐标，由
=
可知M为AB的中点，由中点坐标公式列式求得A，B的坐标，由截距式得直线方程；
（2）由
=2
可知M为线段AB的内分点，且求出分点分线段所成的比，由定比分点公式列式求得A，B的坐标，
由截距式得直线方程；
（3）若|
|=2|
|，可分M为AB的内分点和外分点两种情况求解，为内分点时由（2）得答案，是外分点时由中点坐标公式求得A，B的坐标，由截距式得直线方程．
| AM |
| MB |
（2）由
| AM |
| MB |
由截距式得直线方程；
（3）若|
| AM |
| MB |
解答：
解：M（-2，1），设A（a，0），B（0，b），
（1）若
=
，则M为AB的中点，
由中点坐标公式得：
，解得
．
∴直线L的方程为：-
+
=1，即x-2y+4=0；
（2）若
=2
，则M为线段AB的内分点，且M分线段AB的比λ=2．
由定比分点公式得：
，解得
．
∴直线L的方程为-
+
=1，即x-4y+6=0；
（3）若|
|=2|
|，
当M为线段AB的内分点时，
=2
，
由（2）知，直线L的方程为x-4y+6=0．
当M为线段AB的外分点时，B为AM的中点，
由中点坐标公式得
，解得
．
∴直线L的方程为：
+2y=1，即x+4y-2=0．
（1）若
| AM |
| MB |
由中点坐标公式得：
|
|
∴直线L的方程为：-
| x |
| 4 |
| y |
| 2 |
（2）若
| AM |
| MB |
由定比分点公式得：
|
|
∴直线L的方程为-
| x |
| 6 |
| 2y |
| 3 |
（3）若|
| AM |
| MB |
当M为线段AB的内分点时，
| AM |
| MB |
由（2）知，直线L的方程为x-4y+6=0．
当M为线段AB的外分点时，B为AM的中点，
由中点坐标公式得
|
|
∴直线L的方程为：
| x |
| 2 |
点评：本题考查了直线方程的求法，训练了利用中点坐标公式和定比分点公式求点的坐标，是中低档题．
练习册系列答案
相关题目
已知f（x）是定义在R上的函数且满足f（x）＞-xf′（x），则关于x的不等式f（x-1）＞（x+1）f（x2-1）的解集为（ ）
| A、（-∞，1） |
| B、（-1，1） |
| C、（-∞，0） |
| D、（0，1） |
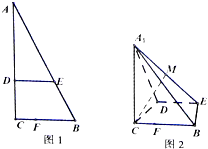如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E，F分别是AC，AB CB上的点，且DE∥BC，DE=2，CF=1，将△ADE沿DE折起到△A1DE的位置，使AC⊥CD，如图2．