题目内容
曲线y=x3的一条切线经过点(2,4),求切点的坐标.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出函数的导数,根据导数的几何意义即可求出切线方程,由切线经过点(2,4),即可解得结论.
解答:
解:设切于点Q(x0,y0),
∵y=x3,
∴y'=3x2,
则切线方程为y-y0=3x02(x-x0),
∵切线经过(2,4),
∴4-
=3x02(2-x0),
即x03-3x02+2=0,
解得 x0=1,或x0=2,∴y0=1或y0=8
∴Q(1,1)或Q(2,8).
∵y=x3,
∴y'=3x2,
则切线方程为y-y0=3x02(x-x0),
∵切线经过(2,4),
∴4-
| x | 3 0 |
即x03-3x02+2=0,
解得 x0=1,或x0=2,∴y0=1或y0=8
∴Q(1,1)或Q(2,8).
点评:本题主要考查导数的几何意义,求出函数的导数即可求出切线斜率,注意区分直线过点的切线和在某点的切线的区别.

练习册系列答案
相关题目
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
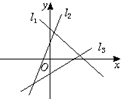

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k3<k2<k1 |
| D、k1<k3<k2 |
用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它需要的小立方块的个数最多是( )
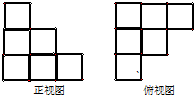

| A、12 | B、13 | C、14 | D、15 |