题目内容
已知函数f(x)=3x的反函数经过点(18,a+2),设g(x)=3ax-4x的定义域为区间[-1,1],
(1)求g(x)的解析式;
(2)若方程g(x)=m有解,求m的取值范围;
(3)对于任意的n∈R,试讨论方程g(|x|)+2|x|+1=n的解的个数.
(1)求g(x)的解析式;
(2)若方程g(x)=m有解,求m的取值范围;
(3)对于任意的n∈R,试讨论方程g(|x|)+2|x|+1=n的解的个数.
考点:反函数
专题:综合题,函数的性质及应用
分析:(1)利用函数与其反函数之间的关系可得a=log32,从而可求得g(x)的解析式;
(2)由g(x)=2x-4x=-(2x-
)2+
,x∈[-1,1],可求得g(x)∈[-2,
],方程g(x)=m有解,从而可得m的取值范围为[-2,
];
(3)由h(x)=g(|x|)+2|x|+1=2|x|-4|x|+2|x|+1=3•2|x|-4|x|可知,h(x)为偶函数,令2x=t,当x∈[0,1]时,1≤t≤2,则y=-t2+3t=-(t-
)2+
(1≤t≤2),利用二次函数的单调性可求得t=
(即x=log23-1)时,ymax=
,t=1或t=2(即x=0或x=1)时,ymin=2,于是可得答案.
(2)由g(x)=2x-4x=-(2x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(3)由h(x)=g(|x|)+2|x|+1=2|x|-4|x|+2|x|+1=3•2|x|-4|x|可知,h(x)为偶函数,令2x=t,当x∈[0,1]时,1≤t≤2,则y=-t2+3t=-(t-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
解答:
解:(1)∵函数f(x)=3x的反函数经过点(18,a+2),
∴3a+2=18,解得:a=log32;
∴g(x)=3ax-4x=3xlog32-4x=2x-4x,x∈[-1,1];
(2)∵g(x)=2x-4x=-(2x-
)2+
,
又x∈[-1,1],
∴
≤2x≤2,0≤2x-
≤
,
∴0≤(2x-
)2≤
,
∴g(x)∈[-2,
],
∵方程g(x)=m有解,∴m的取值范围为[-2,
];
(3)由h(x)=g(|x|)+2|x|+1=2|x|-4|x|+2|x|+1=3•2|x|-4|x|可知,h(x)为偶函数,在[0,1]上,h(x)=3•2x-4x,
令2x=t(1≤t≤2),则y=-t2+3t=-(t-
)2+
(1≤t≤2),
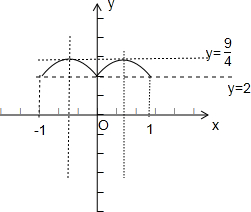
显然,y=-t2+3t=-(t-
)2+
在区间[1,
]上单调递增,在区间[
,2]上单调递减,
∴t=
(x=log23-1)时,ymax=
;
又t=1(即x=0)时,y=2,当t=2(即x=1)时,y=2,
∴t=1或t=2(即x=0或x=1)时,ymin=2.
又n∈R,∴当n>
或n<2时,方程g(|x|)+2|x|+1=n的解的个数为0个;
当n=
时,方程g(|x|)+2|x|+1=n的解的个数为2个;
当n=2时,方程g(|x|)+2|x|+1=n的解的个数为3个;
当2<n<
时,方程g(|x|)+2|x|+1=n的解的个数为4个;
∴3a+2=18,解得:a=log32;
∴g(x)=3ax-4x=3xlog32-4x=2x-4x,x∈[-1,1];
(2)∵g(x)=2x-4x=-(2x-
| 1 |
| 2 |
| 1 |
| 4 |
又x∈[-1,1],
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴0≤(2x-
| 1 |
| 2 |
| 9 |
| 4 |
∴g(x)∈[-2,
| 1 |
| 4 |
∵方程g(x)=m有解,∴m的取值范围为[-2,
| 1 |
| 4 |
(3)由h(x)=g(|x|)+2|x|+1=2|x|-4|x|+2|x|+1=3•2|x|-4|x|可知,h(x)为偶函数,在[0,1]上,h(x)=3•2x-4x,
令2x=t(1≤t≤2),则y=-t2+3t=-(t-
| 3 |
| 2 |
| 9 |
| 4 |

显然,y=-t2+3t=-(t-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
∴t=
| 3 |
| 2 |
| 9 |
| 4 |
又t=1(即x=0)时,y=2,当t=2(即x=1)时,y=2,
∴t=1或t=2(即x=0或x=1)时,ymin=2.
又n∈R,∴当n>
| 9 |
| 4 |
当n=
| 9 |
| 4 |
当n=2时,方程g(|x|)+2|x|+1=n的解的个数为3个;
当2<n<
| 9 |
| 4 |
点评:本题考查函数的性质及综合应用,着重考查函数与其反函数的应用,考查函数的单调性与最值,考查方程解的情况,属于难题.

练习册系列答案
相关题目
已知a=
,函数f(x)=ax,若实数m,n满足f(m)>f(n),?则m,n的关系为( )
| ||
| 2 |
| A、m+n<0 | B、m+n>0 |
| C、m>n | D、m<n |