题目内容
从椭圆上一点A看椭圆的两焦点F1,F2的视角为直角,AF1的延长线交椭圆于点B,且AB=AF2,则椭圆的离心率为 .
考点:椭圆的简单性质
专题:计算题,作图题,圆锥曲线的定义、性质与方程
分析:作图辅助图象,设AB=AF2=m,表示出图中的线段长,利用勾股定理解出m,反代入求椭圆的离心率.
解答:
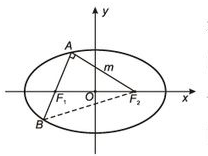 解:如右图:设AB=AF2=m,
解:如右图:设AB=AF2=m,
则AF1=2a-m,F1B=m-(2a-m)=2(m-a),F2B=2a-F1B=4a-2m,
则在Rt△AF1F2中,AF21+AF22=F1F22,即m2+(2a-m)2=(2c)2,
同理,在Rt△ABF2中,2m2=(4a-2m)2,
解得,m=
c,
则(1+
)
c=2
a,
从而e=
=
=
-
.
故答案为:
-
.
 解:如右图:设AB=AF2=m,
解:如右图:设AB=AF2=m,则AF1=2a-m,F1B=m-(2a-m)=2(m-a),F2B=2a-F1B=4a-2m,
则在Rt△AF1F2中,AF21+AF22=F1F22,即m2+(2a-m)2=(2c)2,
同理,在Rt△ABF2中,2m2=(4a-2m)2,
解得,m=
2
| ||
| 3 |
则(1+
| 2 |
2
| ||
| 3 |
| 2 |
从而e=
| c |
| a |
| ||
|
| 6 |
| 3 |
故答案为:
| 6 |
| 3 |
点评:本题考查了数形结合的数学思想,同时考查了椭圆的定义,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
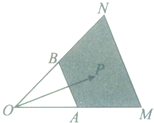 如图
如图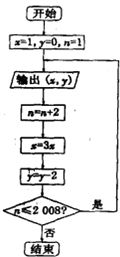 已知某算法的程序框图如图,若将输出的(x,y)值一次记为(x1,y1),(x2,y2),(x3,y3)…,(xn,yn)…若程序进行中输出的一个数对是(x,-8),则相应的x值为( )
已知某算法的程序框图如图,若将输出的(x,y)值一次记为(x1,y1),(x2,y2),(x3,y3)…,(xn,yn)…若程序进行中输出的一个数对是(x,-8),则相应的x值为( )