题目内容
已知二次函数f(x)=ax2+2x+c(a≠0)的图象与y轴交于点(0,1),且满足f(-2+x)=f(-2-x)(x∈R)
(Ⅰ)求该二次函数的解析式及函数的零点.
(Ⅱ)已知函数在(t-1,+∞)上为增函数,求实数t的取值范围.
(Ⅰ)求该二次函数的解析式及函数的零点.
(Ⅱ)已知函数在(t-1,+∞)上为增函数,求实数t的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(I)利用二次函数f(x)=ax2+2x+c(a≠0)的图象与y轴交于点(0,1),可求c的值;根据函数f(x)满足f(-2+x)=f(-2-x)(x∈R),可求a的值,从而可得二次函数的解析式;由f(x)=0,可得函数的零点;
(II)根据函数在(t-1,+∞)上为增函数,且函数图象的对称轴为x=-2,可得t-1≥-2,从而可求实数t的取值范围.
(II)根据函数在(t-1,+∞)上为增函数,且函数图象的对称轴为x=-2,可得t-1≥-2,从而可求实数t的取值范围.
解答:
解:(I)因为二次函数f(x)=ax2+2x+c(a≠0)的图象与y轴交于点(0,1),所以c=1
又因为函数f(x)满足f(-2+x)=f(-2-x)(x∈R),所以x=-
=-2,所以a=
所以二次函数的解析式为:f(x)=
x2+2x+1
由f(x)=0,可得函数的零点为:-2+
,-2-
;
(II)因为函数在(t-1,+∞)上为增函数,且函数图象的对称轴为x=-2,
所以由二次函数的图象可知:t-1≥-2
∴t≥-1.
又因为函数f(x)满足f(-2+x)=f(-2-x)(x∈R),所以x=-
| 2 |
| 2a |
| 1 |
| 2 |
所以二次函数的解析式为:f(x)=
| 1 |
| 2 |
由f(x)=0,可得函数的零点为:-2+
| 2 |
| 2 |
(II)因为函数在(t-1,+∞)上为增函数,且函数图象的对称轴为x=-2,
所以由二次函数的图象可知:t-1≥-2
∴t≥-1.
点评:本题考查二次函数解析式的确定,考查函数的零点,考查函数的单调性,确定函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)是定义在R的偶函数,对任意x∈R,都有f(x+2)=f(2-x)成立,且当x∈[-2,0]时,f(x)=(
)x-1.若关于x0的方程f(x)-loga(x+2)=0在区间(0,6]内恰有两个不同的实数根,则实数a的取值范围为( )
| 1 |
| 2 |
| A、(0,1) | |||
| B、(1,2) | |||
C、(1,
| |||
D、(
|
设集合A,B是全集U的两个子集,则A
B是CUB
CUA的( )
| ? |
| ≠ |
| ? |
| ≠ |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
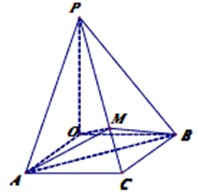 如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=