题目内容
设△ABC的内角A,B,C成等差数列,且满足条件sinAcosC=cos(120°-C)sinC,试判断△ABC的形状,并证明你的结论.
考点:三角形的形状判断
专题:计算题
分析:由三角形ABC中A,B,C成等差数列,利用等差数列的性质列出关系式,再利用三角形内角和定理求出B的度数,以及A+C的度数,用B表示出C,代入已知的等式中,整理后利用两角和与差的正弦函数公式求出sin(A-C)=0,由A和C都为三角形的内角,得出A-C的范围,可得出A-C=0,即A=C,进而确定出此三角形三内角相等,为等边三角形.
解答:
解:△ABC为等边三角形,理由为:
证明:∵△ABC的内角A,B,C成等差数列,
∴A+C=2B,又A+B+C=180°,
∴B=60°,A+C=120°,
∴sinAcosC=cos(120°-C)sinC变形为sinAcosC=cosAsinC,即sin(A-C)=0,
∵-π<A-C<π,∴A=C,
∴A=B=C=60°,
则△ABC为等边三角形.
证明:∵△ABC的内角A,B,C成等差数列,
∴A+C=2B,又A+B+C=180°,
∴B=60°,A+C=120°,
∴sinAcosC=cos(120°-C)sinC变形为sinAcosC=cosAsinC,即sin(A-C)=0,
∵-π<A-C<π,∴A=C,
∴A=B=C=60°,
则△ABC为等边三角形.
点评:此题考查了三角形形状的判断,涉及的知识有:等差数列的性质,两角和与差的正弦函数公式,等边三角形的判定,以及特殊角的三角函数值,熟练掌握性质及公式是解本题的关键.

练习册系列答案
相关题目
若关于x的一元二次不等式kx2+2x-1<0的解集是R,则k的取值范围是 ( )
| A、k<-1 | B、k<0 |
| C、-1<k<0 | D、k>1 |
已知f(x)是定义在R上的函数,并满足f(x)f(x+2)=-2,当1<x<2时,f(x)=x,则f(5.5)=( )
| A、1.5 | B、-1.5 |
| C、5.5 | D、-5.5 |
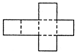 如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )
如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|