题目内容
设f(x)是定义在R的偶函数,对任意x∈R,都有f(x+2)=f(2-x)成立,且当x∈[-2,0]时,f(x)=(
)x-1.若关于x0的方程f(x)-loga(x+2)=0在区间(0,6]内恰有两个不同的实数根,则实数a的取值范围为( )
| 1 |
| 2 |
| A、(0,1) | |||
| B、(1,2) | |||
C、(1,
| |||
D、(
|
考点:根的存在性及根的个数判断,抽象函数及其应用
专题:函数的性质及应用
分析:先画出当x∈[-2,0]时,函数f(x)的图象,根据f(x)是定义在R上的偶函数画出当x∈[0,2]时的函数f(x)的图象.
根据对任意x∈R,都有f(x+2)=f(2-x)成立,可得出f(x)关于直线x=2对称.画出函数y=loga(x+2)的图象,关于x的方程f(x)-loga(x+2)=0在区间(0,6]内恰有两个不同的实数根等价于函数y=f(x)与y=loga(x+2)=0在区间(0,6]内恰有两个不同的交点,据此即可求出实数a的取值范围.
根据对任意x∈R,都有f(x+2)=f(2-x)成立,可得出f(x)关于直线x=2对称.画出函数y=loga(x+2)的图象,关于x的方程f(x)-loga(x+2)=0在区间(0,6]内恰有两个不同的实数根等价于函数y=f(x)与y=loga(x+2)=0在区间(0,6]内恰有两个不同的交点,据此即可求出实数a的取值范围.
解答:
解:(1)①先画出当x∈[-2,0]时,函数f(x)=(
)x-1的图象.
②∵f(x)是定义在R上的偶函数,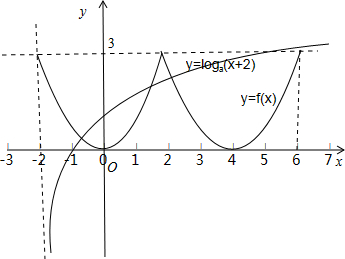
∴当x∈[0,2]时的函数f(x)的图象
与当x∈[-2,0]时,函数f(x)图象关于y轴对称.
③∵对任意x∈R,都有f(x+2)=f(2-x)成立,
∴函数f(x)的图象关于直线x=2对称.
根据以上的分析即可画出函数y=f(x)在区间[-2,6]上的图象.
(2)当0<a<1时,可知不满足题意,应舍去;
当a>1时,画出函数y=loga(x+2)的图象.
若使函数y=f(x)与y=loga(x+2)=0在区间(0,6]内恰有两个不同的交点(即关于x的方程
f(x)-loga(x+2)=0在区间(0,6]内恰有两个不同的实数根),则实数a满足,loga(6+2)>3,∴a3<8,∴a<2,
又1<a,∴1<a<2.
故a的取值范围为1<a<2.
故选B.
| 1 |
| 2 |
②∵f(x)是定义在R上的偶函数,

∴当x∈[0,2]时的函数f(x)的图象
与当x∈[-2,0]时,函数f(x)图象关于y轴对称.
③∵对任意x∈R,都有f(x+2)=f(2-x)成立,
∴函数f(x)的图象关于直线x=2对称.
根据以上的分析即可画出函数y=f(x)在区间[-2,6]上的图象.
(2)当0<a<1时,可知不满足题意,应舍去;
当a>1时,画出函数y=loga(x+2)的图象.
若使函数y=f(x)与y=loga(x+2)=0在区间(0,6]内恰有两个不同的交点(即关于x的方程
f(x)-loga(x+2)=0在区间(0,6]内恰有两个不同的实数根),则实数a满足,loga(6+2)>3,∴a3<8,∴a<2,
又1<a,∴1<a<2.
故a的取值范围为1<a<2.
故选B.
点评:熟练掌握函数的奇偶性、对称性、单调性及数形结合的思想方法是解题的关键.

练习册系列答案
相关题目
若关于x的一元二次不等式kx2+2x-1<0的解集是R,则k的取值范围是 ( )
| A、k<-1 | B、k<0 |
| C、-1<k<0 | D、k>1 |
 设全集U=R,A={y|y=tanx,x∈B},B={x||x|≤
设全集U=R,A={y|y=tanx,x∈B},B={x||x|≤| π |
| 4 |
| A、[-1,1] | ||||
B、[-
| ||||
C、[-1,-
| ||||
D、[-1,-
|