题目内容
6.已知数列{an}满足a1=1,a2=2,an+2=(2+cosnπ)(an-1)+3,n∈N*.那么数列{an}的通项公式为an=$\left\{\begin{array}{l}{n,n为奇数}\\{2×{3}^{\frac{n-2}{2}},n为偶数}\end{array}\right.$.分析 对n分类讨论,利用等差数列与等比数列的通项公式即可得出.
解答 解:an+2=(2+cosnπ)(an-1)+3,n∈N*.
∴当n=2k-1时,an+2=an+2,∴{a2k-1}是等差数列,首项为1,公差为2,∴a2k-1=1+2(k-1)=2k-1,即n为奇数时an=n.
当n=2k时,an+2=3an,∴{a2k}是等比数列,首项为2,公比为3,∴a2k=2×3k-1,即n为偶数时an=$2×{3}^{\frac{n-2}{2}}$.
∴an=$\left\{\begin{array}{l}{n,n为奇数}\\{2×{3}^{\frac{n-2}{2}},n为偶数}\end{array}\right.$.
故答案为:an=$\left\{\begin{array}{l}{n,n为奇数}\\{2×{3}^{\frac{n-2}{2}},n为偶数}\end{array}\right.$.
点评 本题考查了等差数列与等比数列的通项公式、三角函数求值,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.设F1,F2分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,A为双曲线的一个顶点,以F1F2为直径的圆交双曲线的一条渐近线于B,C两点,若△ABC的面积为$\frac{1}{2}{c^2}$,则该双曲线的离心率为( )
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
11.函数y=max{|x+1|,|x-3|}的最小值( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
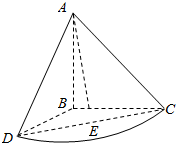 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求: