题目内容
17.设F1,F2分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,A为双曲线的一个顶点,以F1F2为直径的圆交双曲线的一条渐近线于B,C两点,若△ABC的面积为$\frac{1}{2}{c^2}$,则该双曲线的离心率为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 利用△ABC的面积为$\frac{1}{2}$c2,求出双曲线的渐近线的方程,运用点到直线的距离公式,解方程可得c=$\sqrt{2}$a,
即可求出该双曲线的离心率.
解答 解:设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,
即为bx-ay=0,
则A(a,0)到渐近线的距离为d=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$,
由题意,△ABC的面积为$\frac{1}{2}$c2,
则$\frac{1}{2}$•2c•$\frac{ab}{c}$=$\frac{1}{2}$c2,
即为4a2b2=c4,
即有4a2(c2-a2)=c4,
即有c2=2a2,
即c=$\sqrt{2}$a,
则e=$\frac{c}{a}$=$\sqrt{2}$.
故选:D.
点评 本题考查双曲线的离心率,考查三角形面积的计算,同时考查点到直线的距离公式的运用,属于中档题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
12.已知定义在R上的函数y=f(x)对任意的x都满足f(x+2)=f(x),当-1≤x<1时,f(x)=x3.若函数g(x)=f(x)-loga|x|恰有6个不同零点,则a的取值范围是( )
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
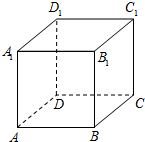 如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)
如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)