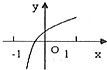题目内容
将曲线方程ρ=
cos(θ-
)化成直角坐标方程: .
| 2 |
| π |
| 4 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由条件根据根据直角坐标和极坐标的互化公式x=ρcosθ、y=ρsinθ,把曲线的极坐标方程化成直角坐标方程.
解答:
解:曲线方程ρ=
cos(θ-
),即 ρ2=ρcosθ+ρsinθ,
化为直角坐标方程为 (x-
)2+(y-
)2=
,
故答案为:(x-
)2+(y-
)2=
.
| 2 |
| π |
| 4 |
化为直角坐标方程为 (x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,属于基础题.

练习册系列答案
相关题目
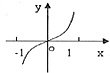
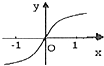
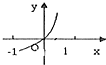
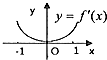 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )
已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )