题目内容
先阅读下面的材料：“求
的值时，采用了如下方法：令
=x，则有x=
，两边同时平方，得x2=1+x，解得x=
（负值舍去）．”----根据以上材料所蕴含的数学思想方法，可以求得函数F（x）=
-x的零点为 ．
1+
|
1+
|
| 1+x |
1+
| ||
| 2 |
3+
|
考点：类比推理
专题：推理和证明
分析：利用类比的方法，令f（x）=
，则F（x）=f（f（f（f（x）））-x．解得即可，
| 3+x |
解答：
解：令f（x）=
，则F（x）=f（f（f（f（x）））-x．若f（x0）=x0，则f（f（x0））=f（x0）=x0，…，f（f（f（f（x0）））=x0；反过来，若x0满足f（f（f（f（x0）））=x0，由于f（x）在[0，+∞）上单调递增，由反证法可知，必有f（x0）=x0．综上可知，
方程f（f（f（f（x）））=x与f（x）=x同解，得x=
（负值舍去）．
故答案为：
| 3+x |
方程f（f（f（f（x）））=x与f（x）=x同解，得x=
1+
| ||
| 2 |
故答案为：
1+
| ||
| 2 |
点评：本题考查类比推理，考查学生的计算能力，解题的关键是掌握类比的方法
练习册系列答案
相关题目
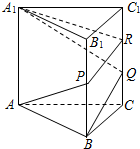已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等．蚂蚁甲从A点沿表面经过棱BB1，CC1爬到点A1，蚂蚁乙从B点沿表面经过棱CC1爬到点A1．如图，设∠PAB=α，∠QBC=β，若两只蚂蚁各自爬过的路程最短，则α+β=