题目内容
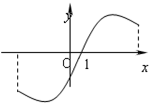 若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中
若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中 ①f(1-x)+f(x+1)=0
②f′(x)(x-1)≥0
③f(x)(x-1)≥0
正确的序号是
考点:利用导数研究函数的单调性
专题:函数的性质及应用,导数的概念及应用
分析:①根据y=f(x+1)是奇函数,运用奇函数的定义即可判断;
②根据图象分析x>1,x<1的图象变化情况,结合导数的符号确定;
③根据图象分析x>1,x<1的图象分布来确定函数值的符号,从而判断正确性.
②根据图象分析x>1,x<1的图象变化情况,结合导数的符号确定;
③根据图象分析x>1,x<1的图象分布来确定函数值的符号,从而判断正确性.
解答:
解:①∵y=f(x+1)是奇函数,
∴由定义得:f(-x+1)=-f(x+1),
即f(1-x)+f(x+1)=0,
故①正确;
②由函数f(x)的图象得:
x>1时,图象有上升,有下降,导数f'(x)先正后负;
x<1时,图象有上升,有下降,导数f'(x)先负后正.
故②错误;
③观察函数f(x)的图象得:
x>1时,图象在x轴上方,f(x)>0;
x<1时,图象在x轴下方,f(x)<0;
故③正确;
故答案为:①③.
∴由定义得:f(-x+1)=-f(x+1),
即f(1-x)+f(x+1)=0,
故①正确;
②由函数f(x)的图象得:
x>1时,图象有上升,有下降,导数f'(x)先正后负;
x<1时,图象有上升,有下降,导数f'(x)先负后正.
故②错误;
③观察函数f(x)的图象得:
x>1时,图象在x轴上方,f(x)>0;
x<1时,图象在x轴下方,f(x)<0;
故③正确;
故答案为:①③.
点评:本题考查运用导数研究函数的单调性,以及函数的奇偶性的定义,考查通过图象分析函数的变化情况,注意函数值与导数值的区别.

练习册系列答案
相关题目
设集合M={-1,0,1},N={x|x2-2x≤0},则M∩N=( )
| A、{-1,0,1} |
| B、{0,1,2} |
| C、{0,1} |
| D、{-1,0} |
育英学校派出5名优秀教师去边远地区的三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有( )
| A、80种 | B、90种 |
| C、120种 | D、150种 |