题目内容
设集合M={-1,0,1},N={x|x2-2x≤0},则M∩N=( )
| A、{-1,0,1} |
| B、{0,1,2} |
| C、{0,1} |
| D、{-1,0} |
考点:交集及其运算
专题:集合
分析:求出N中不等式的解集,找出M与N的交集即可.
解答:
解:由N中的不等式变形得:x(x-2)≤0,
解得:0≤x≤2,即N={x|0≤x≤2},
∵M={-1,0,1},
∴M∩N={0,1}.
故选:C.
解得:0≤x≤2,即N={x|0≤x≤2},
∵M={-1,0,1},
∴M∩N={0,1}.
故选:C.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
下列程序框图的输出结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、“f(0)=0”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、若p:?x0∈R,x02-x0-1>0,则¬p:?x∈R,x2-x-1<0 | ||||||||
| C、若p∧q为假命题,则p,q均为假命题 | ||||||||
D、“若α=
|
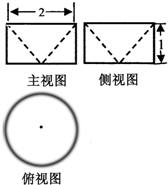 已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )| A、1:4 | B、1:2 |
| C、1:1 | D、2:1 |
已知an=3n+1,n∈N*,如果执行如图的程序框图,那么输出的S等于( )


| A、17.5 | B、35 |
| C、175 | D、350 |
在△ABC中,已知
•
=4,|
|=3,M、N分别是BC边上的三等分点,则
•
的值是( )
| AB |
| AC |
| BC |
| AM |
| AN |
| A、5 | ||
B、
| ||
| C、6 | ||
| D、8 |
已知x,y满足
,则z=x-y的取值范围是( )
|
A、[-
| ||||
| B、[-1,1] | ||||
C、[-
| ||||
D、[-1,
|
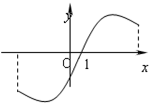 若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中
若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中