题目内容
一个袋中装有6个形状大小完全相同的小球,球的编号分别为1,2,3,4,5,6.
(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取3次,求恰有两次编号为3的倍数的概率;
(Ⅱ)若一次从袋中随机抽取3个球,记球的最大编号为X,求随机变量X的分布列和X的数学期望.
(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取3次,求恰有两次编号为3的倍数的概率;
(Ⅱ)若一次从袋中随机抽取3个球,记球的最大编号为X,求随机变量X的分布列和X的数学期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式
专题:概率与统计
分析:(I)从袋中随机抽取1个球,由已知条件求出其编号为3的倍数的概率,由此能求出有放回的抽取3次,恰有2次编号为3的倍数的概率.
(II)随机变量X所有可能的取值为3,4,5,6.分别求出P(X=3),P(X=4),P(X=5),P(X=6),由此能求出随机变量X的分布列和数学期望.
(II)随机变量X所有可能的取值为3,4,5,6.分别求出P(X=3),P(X=4),P(X=5),P(X=6),由此能求出随机变量X的分布列和数学期望.
解答:
解:(I)从袋中随机抽取1个球,
其编号为3的倍数的概率p=
=
,(2分)
有放回的抽取3次,恰有2次编号为3的倍数的概率为
P3(2)=
(
)2(1-
)=
.(6分)
(II)随机变量X所有可能的取值为3,4,5,6.(7分)
P(X=3)=
=
,P(X=4)=
=
,
P(X=5)=
=
,P(X=6)=
=
,
∴随机变量X的分布列为:
(11分)
EX=3×
+4×
+5×
+6×
=
.(13分)
其编号为3的倍数的概率p=
| 2 |
| 6 |
| 1 |
| 3 |
有放回的抽取3次,恰有2次编号为3的倍数的概率为
P3(2)=
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
| 27 |
(II)随机变量X所有可能的取值为3,4,5,6.(7分)
P(X=3)=
| ||
|
| 1 |
| 20 |
| ||
|
| 3 |
| 20 |
P(X=5)=
| ||
|
| 3 |
| 10 |
| ||
|
| 1 |
| 2 |
∴随机变量X的分布列为:
| X | 3 | 4 | 5 | 6 | ||||||||
| P |
|
|
|
|
EX=3×
| 1 |
| 20 |
| 3 |
| 20 |
| 3 |
| 10 |
| 1 |
| 2 |
| 21 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合的合理运用.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“f(0)=0”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、若p:?x0∈R,x02-x0-1>0,则¬p:?x∈R,x2-x-1<0 | ||||||||
| C、若p∧q为假命题,则p,q均为假命题 | ||||||||
D、“若α=
|
已知x,y满足
,则z=x-y的取值范围是( )
|
A、[-
| ||||
| B、[-1,1] | ||||
C、[-
| ||||
D、[-1,
|
如果loga8>logb8>0,那么a、b间的关系是( )
| A、0<a<b<1 |
| B、1<a<b |
| C、0<b<a<1 |
| D、1<b<a |
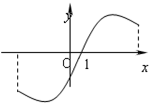 若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中
若函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,则下列结论中